Правила перестановки сумматоров
В общем случае одномерная САУ является многоконтурной, т.е. она содержит произвольное число связанных друг с другом контуров. При преобразовании многоконтурной схемы в эквивалентную одноконтурную руководствуются рядом правил. В их число, прежде всего, входят уже изложенные выше правила замены групп последовательно и параллельно соединенных звеньев, а также звена с обратной связью одним эквивалентным звеном. Кроме того, применяются правила переноса воздействий из одной точки системы в другую и правила перестановки сумматоров. В процессе преобразования многоконтурной САУ часто необходимо переносить суммирующий элемент вперед или назад. Правила переноса сумматоров вытекают из следующих соображений. Пусть сумматор находится на выходе звена с передаточной функцией
Если в (4.6) вынести за скобки
Выражение (4.7) показывает, что на вход звена Таким образом, при переносе суммирующего (вычитающего) элемента назад добавляется звено с обратной передаточной функцией При переносе суммирующего элемента вперед (рис. 4.4, б) аналогично можно показать, что в ветвь добавляется фиктивное звено с передаточной функцией При переносе точки разветвления, т.е. входа параллельной ветви (рис. 4.5), правило преобразования обратное: при переносе этой точки вперед в ветвь добавляется звено с обратной передаточной функцией Из рис. 4.6 следует, что расположенные последовательно сумматоры можно менять местами. При переносе узла через сумматор назад и переносе узла через сумматор вперед необходимо руководствоваться следующими правилами.
Правила перестановки сумматоров поясняет рис. 4.6.
|

 (рис. 4.4, а). При этом справедливо
(рис. 4.4, а). При этом справедливо
 .
.
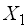 и
и  , чему соответствует эквивалентная схема справа.
, чему соответствует эквивалентная схема справа. .
. .
. Рис. 4.4. Правила переноса сумматора
Рис. 4.4. Правила переноса сумматора
 Рис. 4.5. Правила переноса точки разветвления
Рис. 4.5. Правила переноса точки разветвления
 Рис. 4.6. Правила перестановки сумматоров
Рис. 4.6. Правила перестановки сумматоров
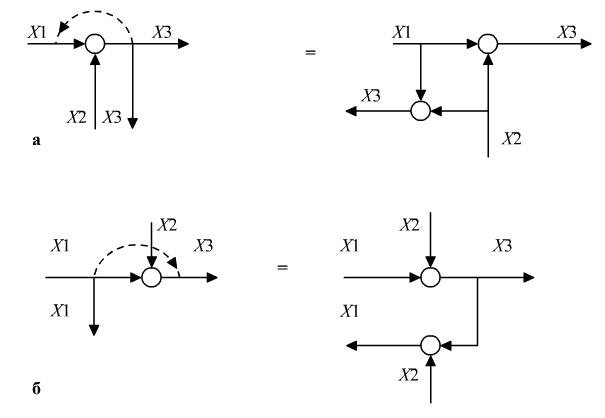 Рис. 4.7. Правила переноса узла через сумматор
Рис. 4.7. Правила переноса узла через сумматор



