Явление сверхпроводимости. Во многих металлах и сплавах и даже в сильно легированных полупроводниках при низких температурах наблюдается необычное явление: ниже некоторой критической
Во многих металлах и сплавах и даже в сильно легированных полупроводниках при низких температурах наблюдается необычное явление: ниже некоторой критической температуры электрическое сопротивление материала неожиданно падает до нуля. Это явление было открыто в 1911 году Камерлинг-Оннесом в ртути и было названо сверхпроводимостью. Оннес хотел выяснить, сколь малым может стать сопротивление вещества электрическому току, если максимально очистить вещество от примесей и максимально снизить «тепловой шум», т.е. уменьшить температуру. Результат этого исследования оказался неожиданным: при температуре ниже 4,15 К сопротивление почти мгновенно исчезло. Материалы, которые находятся в сверхпроводящем состоянии, обладают аномальными физическими свойствами. Перечислим некоторые ил них. 1. Когда вещество находится в сверхпроводящем состоянии, незатухающий электрический ток в нем может существовать как угодно долго. По крайней мере, экспериментально такой незатухающий ток наблюдался в течение двух с половиной лет. 2. При критической температуре происходит фазовый переход из нормального в сверхпроводящее состояние. Теплоемкость вещества в точке фазового перехода испытывает скачок. А при понижении температуры теплоемкость электронного газа стремится к нулю не по линейному, как у нормальных металлов, а по экспоненциальному закону. Соответственно, значение энтропии в сверхпроводящем состоянии ниже значения энтропии в нормальном состоянии. Этот факт свидетельствует о том, что сверхпроводящее состояние более упорядоченное, чем нормальное состояние металла. 3. Необычными оказываются и магнитные свойства вещества в сверхпроводящем состоянии. В 1933 голу Мейнснер и Окенфельд обнаружили, что, если материал, обладающий сверхпроводящими свойствами и помещенный во внешнее магнитное ноле, охладить ниже критической температуры, т.е. перевести его в сверхпроводящее состояние, то в этом состоянии магнитное поле будет выталкиваться из образца. Этот Необходимо подчеркнуть, что свойства, перечисленные в пунктах 2 и 3, принципиально отличают сверхпроводник от идеального проводника. Если даже представить, что электроны в металле имеют бесконечную длину свободного пробега (в реальных веществах такого не бывает) и, следовательно, бесконечную проводимость, то это не приведет к аномальному поведению теплоемкости электронного газа и магнитных свойств металла. Для понимания явления сверхпроводимости развиты два подхода. Многие важные физические свойства сверхпроводников удается описать на основе феноменологических уравнений. Причины же возникновения сверхпроводящего состояния выяснены в микроскопической теории электронов проводимости, взаимодействующих с колебаниями кристаллической решетки (фононами). Здесь следует отметить, что открытое в 1986 году явление высокотемпературной сверхпроводимости (ВТСИ) еще не получило удовлетворительного объяснения на микроскопическом уровне. В 1935 году Ф. Лондон и Г. Лондон установили простое соотношение между полями и токами и первыми исследовали то фундаментальное свойство сверхпроводника, что магнитное ноле не проникает в металл в сверхпроводящем состоянии. Рассмотрим металл с простым параболическим законом дисперсии в зоне проводимости. Представим свободную энергию как сумму трех слагаемых:
Учитывая, что
Где Минимизируя (2), получим следующее уравнение:
Это уравнение называется уравнением Лондонов. Для простейшего линейного случая, когда поверхность образца совпадает с плоскостью
Таким образом, Другая важная характеристика сверхпроводника – длина когерентности, В этой теории вводится квантов механическая «эффективная» волновая функция
Тогда плотность свободной энергии представляется в виде:
В выражении для свободной энергии было введено потенциальное слагаемое:
При Минимизируя
Это соотношение называется уравнением Гинзбурга-Ландау Для плотности тока можно получить следующее выражение:
Уравнение (6) похоже на уравнение Шреденгера, а выражение для плотности тока (7) – на обычное выражение квантово-механическое выражение для плотности тока частиц с массой
|

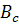 , которое называется критическим полем, сверхпроводимость в веществе исчезает, и вещество становится нормальным металлом. То есть достаточно сильное магнитное поле разрушает сверхпроводимость.
, которое называется критическим полем, сверхпроводимость в веществе исчезает, и вещество становится нормальным металлом. То есть достаточно сильное магнитное поле разрушает сверхпроводимость. (1)
(1)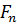 – энергия нормальной составляющей электронного газа,
– энергия нормальной составляющей электронного газа,  – свободная энергия единицы объема конденсированных электронов,
– свободная энергия единицы объема конденсированных электронов, 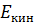 – кинетическая энергия, связанная с незатухающими токами и
– кинетическая энергия, связанная с незатухающими токами и 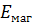 – энергия локального магнитного поля
– энергия локального магнитного поля 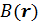 .
.
 – концентрация сверхпроводящих электронов
– концентрация сверхпроводящих электронов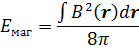
 , получим:
, получим: (2)
(2)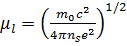 имеет размерность длины.
имеет размерность длины. (3)
(3)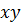 , а поле тангенциально и направлено по оси
, а поле тангенциально и направлено по оси 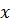 , учитывая уравнения Максвелла, получим следующее решение:
, учитывая уравнения Максвелла, получим следующее решение: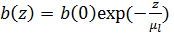 (4)
(4) – глубина проникновения магнитного поля в сверхпроводник.
– глубина проникновения магнитного поля в сверхпроводник.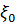 . Уравнение (3) было получено при условии, что скорость электронов и плотность сверхпроводящего тока являются медленноменяющимися функциями расстояния. На длине когерентности эти параметры должны слабо меняться, чтобы было справедливо уравнение Лондонов. Понятие когерентной дины было введено Гинзбургом и Ландау в 1950 году в феноменологической теории сверхпроводимости. Имеет порядок величины расстояния между частицами с коррелированными импульсами.
. Уравнение (3) было получено при условии, что скорость электронов и плотность сверхпроводящего тока являются медленноменяющимися функциями расстояния. На длине когерентности эти параметры должны слабо меняться, чтобы было справедливо уравнение Лондонов. Понятие когерентной дины было введено Гинзбургом и Ландау в 1950 году в феноменологической теории сверхпроводимости. Имеет порядок величины расстояния между частицами с коррелированными импульсами.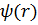 :
: (5)
(5)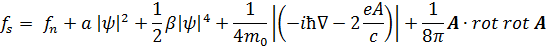
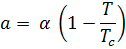
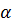 и
и 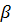 – неизвестные феноменологические константы. Множитель 2 при векторном потенциале учитывает, что в сверхпроводящем состоянии носителями заряда являются пары электронов.
– неизвестные феноменологические константы. Множитель 2 при векторном потенциале учитывает, что в сверхпроводящем состоянии носителями заряда являются пары электронов.
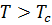 первое слагаемое положительно и доминирует в выражении, что соответствует обычному осциллятору. При
первое слагаемое положительно и доминирует в выражении, что соответствует обычному осциллятору. При 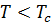 этот член отрицательный и значения
этот член отрицательный и значения  становятся неустойчивыми, что приводит к спонтанному нарушению симметрии.
становятся неустойчивыми, что приводит к спонтанному нарушению симметрии.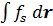 получим следующее уравнение:
получим следующее уравнение: (6)
(6)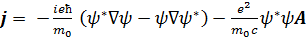 (7)
(7)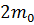 и зарядом
и зарядом 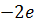 .
.


