Длина когерентности.
Найдем решение (6) в отсутствии поля в линейном случае. Уравнение сведется к виду:
Если в левой части оси x- область нормального состояния, а при
В глубине сверхпроводника:
При малых внешних полях, энергия (9) не изменятся, потому что магнитное поле не проникает вглубь сверхпроводника. Если же поле увеличить настолько, что проигрыш в магнитной энергии (за счет искривления поля вблизи проводника) будет превышать выигрыш в свободной энергии, то металл перейдет в нормальное состояние:
Можно ввести безразмерный параметр В зависимости от параметра Для сверхпроводников первого рода при полях ниже критического, которое увеличивается при снижении температуры, проникновения магнитного поля внутрь сверхпроводника не происходит. При полях больше критического происходит переход в нормальное состояние. В сверхпроводниках второго рода имеется два критических поля. Когда поле больше верхнего критического весь образец переходит в нормальное состояние, когда значение поля Хотя теория Гинзбурга-Ландау была развита до появления БКШ, ее уравнения следуют из микроскопической теории при определенном значении полей и температур. Более того эти уравнения гораздо проще микроскопических и ими обычно пользуются в области их применения. Но теория Гинзбурга-Ландау является феноменологической и не объясняет возникновение сверхпроводящего перехода.
|

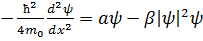 (7’)
(7’) - сверхпроводящего, решение (7’) примет вид:
- сверхпроводящего, решение (7’) примет вид: (8)
(8)
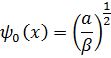
 (9)
(9)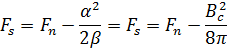

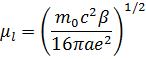
 (10)
(10)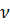 сверхпроводники делятся на сверхпроводники первого (
сверхпроводники делятся на сверхпроводники первого ( )и второго рода (
)и второго рода ( ).
).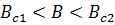 происходит частичное поле проникновения поля в образец, в котором возникает сложная структура чередующихся областей с нормальными и сверхпроводящими типами проводимости (вихревая решетка Абрикосова)
происходит частичное поле проникновения поля в образец, в котором возникает сложная структура чередующихся областей с нормальными и сверхпроводящими типами проводимости (вихревая решетка Абрикосова)


