Модель Вальтера-Лотке.
Рассмотрим математическую модель совместного существования двух биологических видов (популяций) типа "хищник - жертва", называемую моделью Вольтерра - Лотки. Впервые она была получена А.Лоткой (1925 г.), который использовал для описания динамики взаимодействующих биологических популяций. Чуть позже и независимо от Лотки аналогичные (и более сложные) модели были разработаны итальянским математиком В. Вольтерра (1926 г.), глубокие исследования которого в области экологических проблем заложили фундамент математической теории биологических сообществ или так называемой математической экологии. Модель, которую мы рассмотрим, интересна, пожалуй, как раз тем, что с нее, по существу, и началась математическая экология. Пусть есть два биологических вида, которые совместно обитают в изолированной среде. Среда стационарна и обеспечивает в неограниченном количестве всем необходимым для жизни один из видов, который будем называть жертвой. Другой вид - хищник также находится в стационарных условиях, но питается лишь особями первого вида. Это могут быть караси и щуки, зайцы и волки, мыши и лисы, микробы и антитела и т. д.... Будем для определенности называть их карасями и щуками. Караси и щуки живут в некотором изолированном пруду. Среда предоставляет карасям питание в неограниченном количестве, а щуки питаются лишь карасями. у - число щук, х - число карасей. Со временем число карасей и щук меняется, но так как рыбы в пруду много, то не будем различать 1020 карасей или 1021 и поэтому будем считать х и у непрерывными функциями времени t. Надо сказать, что в биологии дело обстоит значительно сложнее, чем, скажем, в механике, где само понятие состояния формализовано и существуют законы Ньютона, позволяющие описать изменение состояния. В биологии этого пока нет. Попробуем из самых простых соображений найти, как меняется состояние (х, у). Рассмотрим x' - скорость изменения численности карасей. Если щук нет, то число карасей увеличивается и тем быстрее, чем больше карасей. Будем считать, что эта зависимость линейная: x' Скорость изменения y' числа щук (если нет карасей), зависит от числа щук y. Будем считать, что y' В экосистеме скорость изменения численности каждого вида также будем считать пропорциональной его численности, но только с коэффициентом, который зависит от численности особей другого вида. Так, для карасей этот коэффициент уменьшается с увеличением числа щук, а для щук увеличивается с увеличением числа карасей. Будем считать эту зависимость также линейной. Тогда получим систему из двух дифференциальных уравнений: x' = Эта система уравнений и называется моделью Вольтерра-Лотки. Числовые коэффициенты Изменяя параметры и решая систему уравнений модели можно исследовать закономерности изменения состояния экологической системы. Именно это позволит вам сделать наша модель, которая находит решение уравнения Вольтерра - Лотки и выводит кривые x(t) и y(t) на экран.
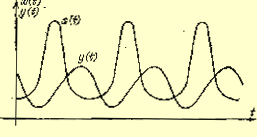
Рисунок 1 Модель Вальтера-Лотке
В качестве примера на рисунке построены кривые изменения численности карасей x и щук y в зависимости от времени t для некоторых типичных значений параметров. Максимумы кривых чередуются, причем максимумы щук отстают от максимума карасей. Это отставание разное для разных экосистем типа "хищник - жертва", но, как правило, много меньше периода колебаний. Получила объяснение периодичность в протекании хронических заболеваний, стало отчасти ясно, почему течение болезни зависит от фазы и интенсивности проводимого лечения. Действительно, как протекает хроническое заболевание? Обострение сменяется улучшением и опять все снова повторяется. Болезнь связана с наличием "хищника" (микроб, вирус), который поедает что-то в организме "жертвы". Обострение бывает, когда "хищника" много - верхние участки кривых на рисунке. Улучшение самочувствия соответствует спадающим участкам, - нижние участки (когда совсем хорошо). И снова наступает ухудшение - возрастающие участки кривой. Обострение тем сильнее, чем больше амплитуда кривой. В состоянии равновесия и около него болезнь слабо выражена. Вы больны, но обострения у вас нет. Наконец, вам надоедает такое состояние, и вы идете к врачу. Врач дает лекарство, вы его принимаете и уничтожаете почти всех "хищников". Сейчас подобные экологические модели строятся при лечении различных хронических заболеваний, в частности, при борьбе с хроническими инфекциями. Строится экологическая модель болезни с учетом всех иммунных факторов и лечение производится в соответствии с этой моделью.
|


 1 x, причем коэффициент
1 x, причем коэффициент 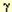 1 yx,
1 yx,