Задание № 6
УТВЕРЖДАЮ Декан факультета социологии и управления _______________доц. Кричинский П.Е.
Индивидуальное задание по производственной практике студента _______________________________________________ _______________________________________________
Руководитель практики: _________________ (подпись)
Ознакомлен: ___________________________ (подпись студента) Индивидуальные задания Задание № 1 Даны точки А, В, С, Д. Найти: 1) координаты точек, симметричных относительно оси Ох точкам А и В, сделать чертёж; 2) координаты точек, симметричных относительно оси Оу точкам С и Д, сделать чертёж; 3) расстояние между точками А и В, С и Д; 4) середину между точками А и С, В и Д.
1.1 А (-4; 7); В (2; 3); С (8; 1); Д (-6; -5);
1.2 А (4; 5); В (2; -3); С (-6; 1); Д (-4; -5);
1.3 А (8; 3); В (-4; -2); С (-6; 7); Д (-2; -8);
1.4 А (3; -2); В (4; 5); С (-7; 8); Д (-8; -3);
1.5 А (4; -1); В (-3; 8); С (-6; -5); Д (9; 4);
1.6 А (-1; -2); В (3; 4); С (7; -6); Д (-5; 10);
1.7 А (5; -3); В (-1; -6); С (9; 2); Д (-7; -4);
1.8 А (11; 4); В (-2; 1); С (-9; -6); Д (-4; 5);
1.9 А (-8; 3); В (5; -7); С (4; 9); Д (-1; -5);
1.10 А (8; 5); В (7; -2); С (-4; -3); Д (-13; 6);
1.11 А (-5; 9); В (4; -3); С (-3; -1); Д (2; 7);
1.12 А (2; 4); В (-6; 5); С (4; -8); Д (-2; -9); 1.13 А(3; -9); В (-6; -3); С (11; 1); Д (14; -5);
1.14 А (15; 3); В (-1; 2); С (-9; -7); Д (5; 6);
1.15 А (7; 8); В (-4; 3); С (-9; -4); Д (10; 5);
1.16 А (4; -7); В (-1; -6); С (8; 9); Д (5; -4);
1.17 А (-4; 2); В (10; -7); С (-2; -8); Д (6; 5);
1.18 А (14; 1); В (-8; 15); С (2; 7); Д (-6; -7);
1.19 А (4; -9); В (-6; 3); С (-6; -5); Д (8; 1);
1.20 А (6; 9); В (-8; 3); С (-4; -7); Д (-6; 5);
1.21 А (5; -4); В (7; 8); С (-9; 6); Д (-1; -4);
1.22 А (-6; -2); В (3; -4); С (8; 10); Д (-5; -8);
1.23 А (12; -3); В (-4; -7); С (-4; 5); Д (8; 3);
1.24 А (-3; -5); В (5; -6); С (7; 9); Д (-9; 10);
1.25 А (7; -9); В (-1; -3); С (5; 11); Д (-7; 9).
Задание № 2 Треугольник АВС задан координатами своих вершин. Найти: 1) уравнение сторон АВ и АС; длину стороны АВ; 2) уравнение и длину высоты СД; 3) уравнение медианы АМ; 4) точку N пересечения медианы АМ и высоты СД; 5) уравнение прямой, проходящей через вершину с параллельно стороне АВ; 6) расстояние от точки В до прямой АС; 7) угол при вершине А; 8) координаты точки Р, расположенной симметрично точке А относительно прямой СД.
2.1 А (-6; -4); В (-10; -1); С (6; 1);
2.2 А (12; 0); В (18; 8); С (0; 5);
2.3 А (-2; 2); В (-6; -3); С (10; -1);
2.4 А (8; 2); В (14; 10); С (-4; 7);
2.5 А (2; -4); В (-2; -1); С (14; 1);
2.6 А (2; -1); В (8; 7); С (0; 4);
2.7 А (5; -3); В (1; 0); С (17; 2);
2.8 А (14; -6); В (20; 2); С (2; -1);
2.9 А (3; 4); В (-1; 7); С (15; 9);
2.10 А (1; -2); В (7; 6); С (-11; 3);
2.11 А (-8; -3); В(4; -12); С (8; 10); 2.12 А (-5; 7); В (7; -2); С (11; 20);
2.13 А (-12; -1); В (0; -10); С (4; 12);
2.14 А (-10; 9); В (2; 0); С (6; 22);
2.15 А (0; 2); В (12; -7); С (16;15);
2.16 А (-9; 6); В (3; -3); С (7; 19);
2.17 А (1; 0); В (13; -9); С (17; 13);
2.18 А (-4; 10); В (8; 1); С (12; 23);
2.19 А (2; 5); В (14; -4); С (18; 18);
2.20 А (-1; 4); В (11; -5); С (15; 17);
2.21 А (-2; 7); В (10; -2); С (8; 12);
2.22 А (-6; 8); В (6; -1); С (4; 13);
2.23 А (3; 6); В (15; -3); С (13; 11);
2.24 А (-10; 5); В (2; -4); С (0; 10);
2.25 А (-4; 12); В (8; 3); С (6; 17).
Задание № 3 Найти координаты центра и радиус окружности. Выполнить чертёж.
3.1 x 2 + y 2 – 8 x + 12 y – 29 = 0.
3.2 x 2 + y 2 + 16 x – 20 y – 5 = 0.
3.3 x 2 + y 2 – 4 x + 4 y – 8 = 0.
3.4 x 2 + y 2 + 6 x – 4 y – 62 = 0.
3.5 x 2 + y 2 + 6 x – 14 y – 6 = 0.
3.6 x 2 + y 2 – 24 x + 2 y – 51= 0.
3.7 x 2 + y 2 – 4 x + 16 y – 5 = 0.
3.8 x 2 + y 2 + 12 x – 10 y + 45 = 0.
3.9 x 2 + y 2 – 8 x + 6 y = 0.
3.10 x 2 + y 2 + 12 x – 14 y + 49 = 0.
3.11 x 2 + y 2 – 18 x + 2 y – 39 = 0.
3.12 x 2 + y 2 + 8 x – 4 y – 5 = 0.
3.13 x 2 + y 2 – 6 x + 14 y – 6 = 0.
3.14 x 2 + y 2 – 4 x + 8 y – 5 = 0.
3.15 x 2 + y 2 + 8 x – 12 y – 29 = 0.
3.16 x 2 + y 2 – 16 x + 20 y – 5 = 0.
3.17 x 2 + y 2 + 4 x + 4 y – 8 = 0.
3.18 x 2 + y 2 + 24 x –2 y – 51= 0.
3.19 x 2 + y 2 – 12 x + 14 y – 15 = 0.
3.20 x 2 + y 2 – 10 x + 16 y – 11 = 0.
3.21 x 2 + y 2 + 8 x – 6 y – 24 = 0.
3.22 x 2 + y 2 – 12 x + 8 y – 29 = 0.
3.23 x 2 + y 2 + 10 x – 4 y + 13 = 0.
3.24 x 2 + y 2 – 8 x + 6 y – 24 = 0.
3.25 x 2 + y 2 – 4 x + 16 y + 67 = 0.
Задание № 4 Привести уравнение кривой к каноническому виду, указать вершины, найти фокусы и эксцентриситет кривой (для гиперболы найти уравнения асимптот). Построить кривую.
4.1 а) x 2 + y 2 – 36 = 0; б) 9 x 2 – 49 y 2 – 441 = 0;
4.2 а) 9 x 2 + 16 y 2 – 144 = 0; б) 25 x 2 – 81 y 2 – 225 = 0;
4.3 а) 4 x 2 + 9 y 2 – 36 = 0; б) 81 x 2 – 64 y 2 – 1600 = 0;
4.4 а) 16 x 2 + 25 y 2 – 400 = 0; б) 100 x 2 – 9 y 2 – 900 = 0;
4.5 а) 25 x 2 + 36 y 2 – 900 = 0; б) 9 х 2 – y 2 – 81 = 0;
4.6 а) 4 x 2 + 25 y 2 – 100 = 0; б) 64 x 2 – y 2 – 64 = 0;
4.7 а) 9 x 2 + 25 y 2 – 225 = 0; б) 81 x 2 – 16 y 2 – 1296 = 0;
4.8 а) 4 x 2 + 9 y 2 – 144 = 0; б) 25 x 2 – 16 y 2 - 400= 0;
4.9 а) 25 x 2 + 49 y 2 – 1225 = 0; б) 4 x 2 – y 2 – 36 = 0;
4.10 а) 4 x 2 + 81 y 2 – 324 = 0; б) 9 x 2 – y 2 – 36 = 0;
4.11 а) 9 x 2 + 49 y 2 – 441 = 0; б) 36 x 2 – 25 y 2 – 900 = 0;
4.12 а) x 2 + 16 y 2 – 64 = 0; б) 25 x 2 – 9 y 2 – 225 = 0;
4.13 а) 9 x 2 + 100 y 2 – 900 = 0; б) 16 x 2 – 49 y 2 – 784 = 0;
4.14 а) 25 x 2 + 81 y 2 – 2025 = 0; б)16 x 2 – 9 y 2 – 144 = 0;
4.15 а) 4 x 2 + 49 y 2 – 196 = 0; б) 4 x 2 – y 2 – 64 = 0;
4.16 а) 9 x 2 + 64 y 2 – 576 = 0; б) 25 x 2 – 4 y 2 – 400 = 0;
4.17 а) 16 x 2 + 81 y 2 – 1296 = 0; б) 9 x 2 – 4 y 2 - 36= 0;
4.18 а) x 2 + 25 y 2 – 100 = 0; б) 81 x 2 – 4 y 2 – 324 = 0;
4.19 а) 25 x 2 + 64 y 2 – 1600 = 0; б) 16 x 2 – y 2 – 64 = 0;
4.20 а) x 2 + 9 y 2 – 36 = 0; б) 49 x 2 – 25 y 2 – 1225 = 0;
4.21 а) 16 x 2 + 4 y 2 – 784 = 0; б) 25 x 2 – 4 y 2 – 100 = 0;
4.22 а) x 2 + 9 y 2 – 81 = 0; б) 49 x 2 – 4 y 2 – 196 = 0;
4.23 а) x 2 + 4 y 2 – 64 = 0; б) 64 x 2 – 9 y 2 – 576 = 0;
4.24 а) 4 x 2 + 25 y 2 – 400 = 0; б) 9 x 2 – 4 y 2 – 144 = 0;
4.25 а) x 2 + 100 y 2 – 25 = 0; б) 81 x 2 – 25 y 2 – 2025 = 0.
Задание № 5 Даны уравнения парабол. 1. Указать ось симметрии. 2. Найти координаты фокуса и написать уравнение директрисы для каждой из парабол. 3. Построить графики заданных парабол.
5.1 а) у 2 – 16 х = 0; б) х 2 + 4 у = 0;
5.2 а) х 2 – 9 у = 0; б) у 2 + 10 х = 0;
5.3 а) у 2 + 4 х = 0; б) х 2 – 18 у = 0;
5.4 а) х 2 – 12 у = 0; б) у 2 + 6 х = 0;
5.5 а) у 2 – 14 х = 0; б) х 2 + 8 у = 0;
5.6 а) х 2 + 10 у = 0; б) у 2 – 16 х = 0;
5.7 а) у 2 – 6 х = 0; б) х 2 + 18 у = 0;
5.8 а) х 2 – 2 у = 0; б) у 2 + 16 х = 0;
5.9 а) у 2 – 10 х = 0; б) х 2 + 4 у = 0;
5.10 а) х 2 – 32 у = 0; б) у 2 + 12 х = 0;
5.11 а) у 2 – 4 х = 0; б) х 2 + 16 у = 0;
5.12 а) у 2 – 48 х = 0; б) х 2 + 8 у = 0;
5.13 а) х 2 – 10 у = 0; б) у 2 + 6 х = 0;
5.14 а) у 2 – 32 х = 0; б) х 2 + 6 у = 0;
5.15 а) х 2 – 14 у = 0; б) у 2 + 12 х = 0;
5.16 а) у 2 – 22 х = 0; б) х 2 + 18 у = 0;
5.17 а) х 2 – 2у = 0; б) у 2 + 6 х = 0;
5.18 а) у 2 – 18 х = 0; б) х 2 + 34 у = 0;
5.19 а) у 2 – 48 х = 0; б) х 2 + 28 у = 0;
5.20 а) у 2 – 12 х = 0; б) х 2 + 20 у = 0;
5.21 а) х 2 – 24 у = 0; б) у 2 + 8 х = 0;
5.22 а) у 2 – 26 х = 0; б) х 2 + 12 у = 0;
5.23 а) у 2 – 36 х = 0; б) х 2 + 44 у = 0;
5.24 а) х 2 + 20 у = 0; б) у 2 – х = 0;
5.25 а) у 2 – 64 х = 0; б) х 2 + 5 у = 0.
Задание № 6 Составить канонические уравнения: а) эллипса; б) гиперболы; в) параболы (А, В – точки, лежащие на кривой, F – фокус, а – большая (действительная) полуось, b – малая (мнимая) полуось, e – эксцентриситет, у = ± kx – уравнение асимптот гиперболы, D – директриса кривой, 2 с – фокусное расстояние).
6.1 а) b = 15, F (-10, 0); б) a = 13, e = 14/13; в) D: x = -4.
6.2 а) b = 2, F (4 в) D: x = 5.
6.3 a) А (3, 0) B (2, в) D: y = -2.
6.4 a) e = в) D: y = 1.
6.5 a) 2 a = 22, e = в) ось Oх, А (27, 9).
6.6 а) b = в) ось Oу, А (4, -8).
6.7 а) а = 4, F = (3, 0); б) b = 2 в) D: x = -2.
6.8 a) b = 4, F = (9, 0); б) a = 5, e = 7/5; в) D: x = 6.
6.9 a) A (0, в) D: y = -4. 6.10 a) e = 7/8, A (8, 0); б) A (3, -
6.11 a) 2 a = 24, e = в) ось Oх, А (-7, -7).
6.12 а) b = 2, e = 5 в) ось Oх, А (-5, 15).
6.13 а) а = 6, F (-4, 0); б) b = 3, F (7, 0); в) D: x = -7.
6.14 a) b = 7, F (5, 0); б) а = 11, e = 12/11; в) D: x = 10.
6.15 в) D: y = 1.
6.16 a) e = 3/5, A (0, 8); б) А (Ö6, 0), В (-2 в) D: y = 9.
6.17 a) 2 a = 22, e = 10/11; б) k = Ö11/5, 2 c = 12; в) ось Oх, А (-7, 5).
6.18 а) b = 5, e = 12/13; б) k = 1/3, 2 a = 6; в) ось Oу, А (-9, 6).
6.19 а) а = 9, F (7, 0); б) b = 6, F (12, 0); в) D: x = -1/4.
6.20 a) b = 5, F (-10, 0); б) a = 9, e = 4/3; в) D: x = 12.
6.21 a) A (0, -2), F ( в) D: y =5.
6.22 a) e = 2/3, A (-6, 0); б) А ( в) D: y = 1.
6.23 a) 2 a = 50, e = 3/5; б) k = в) ось Oу, А (4, 1).
6.24 а) b = 2 в) ось Oу, А (-2, 3
6.25 а) а = 13, F (-5, 0); б) b = 44, F (-7, 0); в) D: x = -3/8.
|

 , 0); б) a = 7, e =
, 0); б) a = 7, e =  /7;
/7;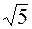 /3) б) k = 3/4, c = 5/4;
/3) б) k = 3/4, c = 5/4; /5, A (-5, 0); б) A (
/5, A (-5, 0); б) A ( , 3), B (4
, 3), B (4 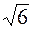 , 3
, 3  /11; б) k = 2/3, 2 c = 10
/11; б) k = 2/3, 2 c = 10  ;
;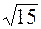 , e =
, e =  /25; б) k = 3/4, 2 a = 16;
/25; б) k = 3/4, 2 a = 16; ), B (
), B (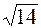 /3, 1); б) k =
/3, 1); б) k =  /6; б) k =
/6; б) k = 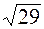 /29; б) k = 12/13, 2 a = 26;
/29; б) k = 12/13, 2 a = 26; a) A (-Ö17/3, 1/3), B (
a) A (-Ö17/3, 1/3), B (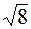 , 0), B (
, 0), B (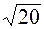 /3, 2);
/3, 2);


