Более сложные модели освещения
Когда мы рассматривали алгоритмы удаления невидимых линий, предполагалось, что сцена включает только непрозрачные объекты. В простой модели освещения тоже речь шла о непрозрачных поверхностях. Теперь можно усложнить задачу, включив в модель не только отражение света, но и преломление. При переходе луча из одной среды в другую его направление изменяется согласно закону Синеллиуса: преломленный луч лежит в плоскости, образуемой нормалью к плоскости и падающим лучом, а углы, образуемые лучами с нормалью, связаны формулой
где
Рис. 10.7. Преломленный и отраженный лучи
Рис. 10.8. Преломление в призме При наличии в пространственной сцене прозрачных или полупрозрачных объектов надо учитывать, что изображение других объектов будет отличаться от обычной проекции на картинную плоскость (рис. 10.8). Эти эффекты хорошо знакомы всем, кто сталкивался с различными линзами. Для построения изображения таких сцен целесообразно использовать алгоритмы с обратной трассировкой лучей. Для изображения полупрозрачных поверхностей без учета преломления можно ввести так называемый коэффициент прозрачности
При Устранение ступенчатости (антиэлайзинг) При построении растрового образа линий (см. лекцию 9) мы сталкиваемся с эффектом ступенчатости, связанным с дискретизацией непрерывного объекта. Искажение идеального образа происходит потому, что из всего множества точек мы выбираем только те, которые оказываются ближе всего к центру элемента растра, и инициализируем этот элемент.
Рис. 10.9. Распределение весов при увеличении разрешения в 4 раза
Рис. 10.10. Распределение весов при увеличении разрешения в 16 раз Для предотвращения сильных искажений в этом случае можно, во- первых, повышать разрешение растра, что позволяет отображать всё более мелкие детали объектов. Но у этого подхода есть свои чисто физические ограничения. Второй подход заключается в том, что растр рассчитывается с более высоким разрешением, а изображается с более низким - путем усреднения атрибутов пикселей первого более детального растра с определенными весами. Если веса одинаковы, то мы получаем равномерное усреднение, как показано на рис. 10.9. Лучших результатов можно достигнуть, если использовать разные веса у пикселей первого растра. На рис. 10.10 показано распределение весов при детализации пикселя экранного растра. Другой метод устранения ступенчатости состоит в том, чтобы рассматривать пиксель не как точку, а как некоторую конечную область. В алгоритмах построения растровой развертки пиксель считается принадлежащим области закрашивания, если его центр находился внутри идеального образа области. Если рисунок черно-белый, то устранить эффект ступенчатости растра практически невозможно. Но при наличии оттенков полутонов можно задать интенсивность цвета пикселя в зависимости от площади его пересечения с областью. Рассмотрим применение этого метода на примере раскраски многоугольника. Ребро многоугольника строится с использованием алгоритма Брезенхема, описанного в лекции 9. Здесь в этот алгоритм будут внесены изменения, включающие параметр максимального числа уровней интенсивностей. Определяя принадлежность пикселя многоугольнику, мы будем использовать в качестве ошибки e долю площади, принадлежащей идеальной фигуре (рис. 10.11).
Рис. 10.11. Отсекаемая отрезком площадь пикселя Рассмотрим опять случай, когда отрезок направлен в положительный квадрант координатной плоскости под углом, меньшим Устранение эффекта ступенчатости с математической точки зрения является задачей сглаживания. Приведенный здесь алгоритм, использующий площади пересечения растра и идеального образа, можно описать с помощью операции свертки функции. Сначала дадим необходимые определения. Сверткой функции
Функция Рассмотрим в качестве свертываемой функции и ядра следующие функции:
Рис. 10.12. Блок-схема модифицированного алгоритма Брезенхема Тогда, в силу того, что подынтегральное выражение обращается в ноль при
Учитывая вид функции
Очевидно, что наша свертка дает площадь пересечения треугольника, образованного свертываемой функцией с квадратом, основание которого есть отрезок
Рис. 10.13. Фигуры, соответствующие значениям свертки из таблицы 10.1 На рис. 10.13 приведен вид пересечения для всех пяти случаев из таблицы 10.1. Если сравнить эти результаты с рис. 10.11, то видно, что значения свертки при В заключение проиллюстрируем результат применения алгоритма устранения ступенчатости на примере изображения, полученного с помощью программы Corel Draw. Эта программа представляет собой развитый графический редактор, позволяющий строить объекты векторной графики. На рис. 10.14 показано изображение простых графических примитивов, предварительно переведенное в растровую форму, на котором при большом увеличении заметно сглаживание с применением оттенков серого цвета.
Рис. 10.14. Сглаженные изображения Вопросы и упражнения
|


 - показатели преломления двух сред (рис. 10.7). Пропускание света также может быть диффузным (если часть энергии света рассеивается средой) или направленным. В первом случае мы имеем дело с полупрозрачными телами, которые изменяют окраску видимых сквозь них объектов. Во втором случае тело является прозрачным, и оно визуально обнаруживается только благодаря искажениям объектов за счет преломления лучей.
- показатели преломления двух сред (рис. 10.7). Пропускание света также может быть диффузным (если часть энергии света рассеивается средой) или направленным. В первом случае мы имеем дело с полупрозрачными телами, которые изменяют окраску видимых сквозь них объектов. Во втором случае тело является прозрачным, и оно визуально обнаруживается только благодаря искажениям объектов за счет преломления лучей.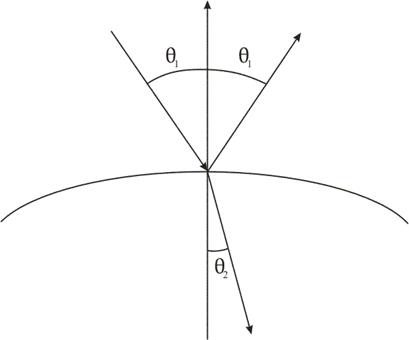

 , который позволяет смешивать интенсивности для видимой поверхности и той, что расположена за ней:
, который позволяет смешивать интенсивности для видимой поверхности и той, что расположена за ней:
 поверхность непрозрачна, при
поверхность непрозрачна, при  - полностью прозрачна. Для полупрозрачных тел необходимо учитывать их объемную структуру.
- полностью прозрачна. Для полупрозрачных тел необходимо учитывать их объемную структуру.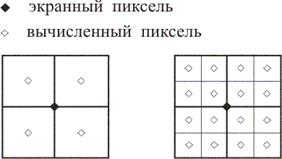


 . Идеальный отрезок при заданном значении целочисленной координаты
. Идеальный отрезок при заданном значении целочисленной координаты  может пересекать один или два пикселя. В предыдущей версии алгоритма выбирался пиксель, центр которого располагался ближе к отрезку. Теперь интенсивность для обоих пикселей будет задаваться в зависимости от степени близости каждого из них. Инициализация пикселя будет использовать интенсивность в качестве параметра. Предполагается, что отрезок начинается с угла первого пикселя, исходя из чего и задается начальная интенсивность. Блок-схема алгоритма приведена на рис. 10.12.
может пересекать один или два пикселя. В предыдущей версии алгоритма выбирался пиксель, центр которого располагался ближе к отрезку. Теперь интенсивность для обоих пикселей будет задаваться в зависимости от степени близости каждого из них. Инициализация пикселя будет использовать интенсивность в качестве параметра. Предполагается, что отрезок начинается с угла первого пикселя, исходя из чего и задается начальная интенсивность. Блок-схема алгоритма приведена на рис. 10.12. называется интеграл вида
называется интеграл вида
 называется ядром свертки. В качестве ядра свертки обычно используется либо функция с конечным носителем (т.е. отличная от нуля лишь на некотором конечном интервале), либо быстро убывающая на бесконечности функция (это может являться необходимым условием существования интеграла).
называется ядром свертки. В качестве ядра свертки обычно используется либо функция с конечным носителем (т.е. отличная от нуля лишь на некотором конечном интервале), либо быстро убывающая на бесконечности функция (это может являться необходимым условием существования интеграла).

 и при
и при  , получаем
, получаем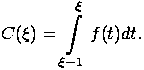
 , получаем, что свертка будет отлична от нуля только на интервале
, получаем, что свертка будет отлична от нуля только на интервале  . Значения свертки в некоторых точках приведены в таблице 10.1.
. Значения свертки в некоторых точках приведены в таблице 10.1.

 на оси
на оси  .
.
 дают площадь той части пикселя, что находится внутри многоугольника (если считать
дают площадь той части пикселя, что находится внутри многоугольника (если считать  ), а при
), а при  - сумму площадей двух пересекаемых пикселей.
- сумму площадей двух пересекаемых пикселей.



