Департамент образования и науки Тюменской области
мошки комары мокрецы москиты Относительно резкий переход между двумя природными сообщества, согласно Ф. Клементсу носит название: биотоп экотоп эдафотоп экотон Межпопуляционные форические связи, возникающие при транспортировке одних организмов другими, как, например перенос птицами семян и спор носят также название: зоохория трансмиссивность интродукция аллогенная сукцессия Какое из перечисленных утверждений будет справедливым согласно правилу Аллена: Среди трех видов лисиц (арктического, европейского и африканского), самые короткие уши будет иметь арктический вид Среди трех видов лисиц (арктического, европейского и африканского), самые короткие уши будет иметь африканский вид Среди трех видов лисиц (арктического, европейского и африканского), наибольшую массу будет иметь арктический вид Среди трех видов лисиц (арктического, европейского и африканского), наименьшую массу будет иметь арктический вид Какое из перечисленных утверждений будет справедливым согласно правилу Бергмана: Среди трех видов лисиц (арктического, европейского и африканского), самые короткие уши будет иметь арктический вид Среди трех видов лисиц (арктического, европейского и африканского), самые короткие уши будет иметь африканский вид Среди трех видов лисиц (арктического, европейского и африканского), наибольшую массу будет иметь арктический вид Среди трех видов лисиц (арктического, европейского и африканского), наименьшую массу будет иметь арктический вид Расширение закона минимума до закона действия факторов, согласно которому состав и структура экосистемы определяется фактором, приближающимся к минимуму, ведено: А. Тинеманом Ю. Либихом Б. Коммонером К. Бергманом Закон, согласно которому отсутствие или недостаток некоторых (не фундаментальных) экологических факторов может быть компенсировано другими близкими факторами, сформулирован: К Бергманом Ю. Либихом Э. Рюбелем В. Шелфордом Появление «системного эффекта» - особых новых свойств в системе со системообразующими связями, неприсущих ее составным элементам и не являющееся их простой суммой, носит название: эмерджентность правило экологической пирамиды эвристический принцип принцип Ле-Шателье-Брауна Сокращение вдвое числа часовых поясов в России при сохранении неизменной разницы между московским временем и гринвичским меридианом приведет: к росту проявлений десинхроноза преимущественно в юго-западных регионах к росту проявлений десинхроноза преимущественно в юго-восточных регионах к росту проявлений десинхроноза преимущественно в северо-западных регионах к росту проявлений десинхроноза преимущественно в северо-восточных регионах Термин «биоценоз» был предложен в 1877 году: А. Тенсли В.Н. Сукачевым К. Мёбиусом Ю. Одумом Экотоп включает в себя следующие компоненты: климат и геологическую среду: почвогрунтовой компонент (эдафотоп) биоценоз и геологическую среду: почвогрунтовой компонент (эдафотоп) биотоп и биоценоз биоценоз и климат Побочными эффектами «зелёной революции» (термин В. Гауда, 1968) явились: засоление почвы, загрязнение среды фторхлоруглеводородами и эвтрофикация опустынивание и загрязнение почвы солями тяжелых металлов засоление почвы, опустынивание и загрязнение среды фторхлоруглеводородами (ФХ) вытеснение естественных растений генно-модифицированными видами и нитрификация Приспособляемость живого организма к изменениям условий среды носит название: адаптивность экологическая валентность емкость экосистемы демографический потенциал Закон одного процента в экологии гласит: в каждом звене последующем звене экологической пирамиды биомасса составляет 1% от предыдущего изменение энергетики природной системы в пределах до 1% всегда выводит систему из равновесия изменение энергетики природной системы в пределах до 1%, как правило, не выводит систему из равновесия все продуценты потребляют не более 1% от солнечной энергии Необходимыми участниками механизма Чэпмана, описывающего образование и разрушение озонового слоя, помимо O2, также являются: O (атомарный кислород), O3 и ультрафиолетовое излучение атомарный водород (H), O3 и ультрафиолетовое излучение O (атомарный кислород), вода и солнечный свет ультрафиолетовое излучение, вода и O3 В каком каталитическом цикле разрушения озонового слоя задействованы хлорфторуглероды, имеющие в значительной степени антропогенное происхождение: Галогеновом кислородномазотномводородном Количество хромосом в кариотипе при синдроме Патау: 47 Главным центром нервной регуляции циркадианной системы млекопитающих является: эпифиз гипоталамус гипофиз ЦНС В кариотипе человека преобладают хромосомы: метацентрические субметацентрические акроцентрические телоцентрические Зависимость массы представителя данного вида от географической широты обитания изложена в: правиле Бергмана фотопериодическом правиле Ашоффа правиле Аллена законе экологических пирамид энергий Линдемана Человек не является промежуточным хозяином для: Echinococcus granulosus Dicrocoelium lancaetum Taenia solium Hymenolepis nana Полный метаморфоз свойственен: Hyalomma marginatum Sarcoptes scabiei Phlebotomus pappatassii Strongyloides stercoralis Для филяриатозов характерен путь заражения: пищевой фекально-оральный контактно-бытовой трансмиссивный алиментарный Автором учения о девастации является: В.А. Догель А.Н. Павловский К.И. Скрябин А.Н. Северцов Филяриатозом является: дракункулез стронгилоидоз онхоцеркоз бруцеллез Неполный метаморфоз свойственен: Dermanyssus gallinae Pulex irritans Phtirus pubis Wohlfartia magnifica Законом Коммонера не является: все со всем связано человек не должен ждать милости от Природы ничто не дается даром Природа знает лучше Реакция Браше позволяет выявить в клетке: ДНК РНК гликоген липиды
Ответы: 1). определитель, полученный вычеркиванием ой строки и го столбца, умноженный на 2). определитель, полученный вычеркиванием го столбца и ой строки 3). матрица, полученная из исходной вычеркиванием го столбца и ой строки 4). определитель, полученный вычеркиванием ой строки и го столбца 5). матрица, полученная из исходной вычеркиванием ой строки и го столбца 2. ##2.8.27.1(1) При каком значении Ответы: 1). 3. ##4.2.9.1(2) Найти производную функции Ответы: 1). 4. ##4.7.10.1(3) Найти производную Ответы: 1). 5. ##5.8.5.1(2) Найти Ответы: 1). 6. ##1.9.55.2(4) Вычислить объем параллелепипеда Ответы: 1). 7. ##2.2.38.2(3) Составить уравнение прямой, проходящей через точку пересечения прямых Ответы: 1). 8. ##2.6.18.2(4) Написать уравнение плоскости, которая содержит ось Ответы: 1). 9. ##3.5.12.2(2) Вычислить предел функции Ответы: 1). 0 2). -1 3). нет правильного ответа------- 4). 10. ##3.7.45.2(2) Используя определения непрерывности функции в точке, найти такие значения Ответы: 1). 11. ##4.3.28.2(2) Найти производную функции Ответы: 1). 12. ##5.5.18.2(4) Задана функция Ответы: 1). 13. ##5.7.24.2(1) Найти полную производную функции – Ответы: 1). 14. ##2.4.134.3(1) Уравнение директрисы параболы Ответы: 1). 15. ##4.9.16.2(2) Удовлетворяют ли функции Ответы: 1). Да,
Вариант №4 1. ##1.2.1.1(1) Закончить утверждение. Определитель матрицы Ответы: 1). 2. ##1.9.24.1(2) Найти смешанное произведение векторов Ответы: 1). 3. ##2.8.39.1(1) Дан треугольник Ответы: 1). 4. ##4.2.1.1(4) Найти производную функции Ответы: 1). 5. ##4.7.11.1(1) Найти производную Ответы: 1). 6. ##1.5.21.2(3) Определить, имеет ли система решение, если да, то решить систему уравнений по формулам Крамера Ответы: 1). бесчисленное множество решений 2). 7. ##3.7.35.2(5) Используя определения непрерывности функции в точке, найти такие значения Ответы: 1). 8. ##4.3.1.1(2) Значение производной функции Ответы: 1). 9. ##5.5.21.2(4) Задана функция Ответы: 1). 10. ##5.7.23.2(1) Найти Ответы: 1). нет правильного ответа 2). 11. ##2.4.188.3(2) Вывести уравнение геометрического места точек, сумма расстояний от которых до двух данных точек Ответы: 1). 12. ##2.10.28.3(2) Найти проекцию точки Ответы: 1). 13. ##4.9.13.2(3) Удовлетворяет ли функция Ответы: 1). Да, 14. ##4.10.30.1(2) Вычислить предел, используя правило Лопиталя Ответы: 1). 15. ##4.12.57.3(3) Если в некоторой окрестности точки Ответы: 1).
Вариант №5 1. ##1.1.60.1(2) Дано: Ответы: 1). 2. ##1.2.11.1(2) Вставить пропущенное. Минором Ответы: 1). определитель, полученный вычеркиванием 3. ##1.8.42.1(1) Найти векторное произведение векторов Ответы: 1). 4. ##2.2.1.1(2) Написать уравнение прямой, проходящей через точку Ответы: 1). 5. ##2.4.47.1(3) Уравнение Ответы: 1). окружность 2). параболу 3). две пересекающиеся прямые 4). эллипс 5). гиперболу 6. ##2.5.22.1(3) Расстояние от точки Ответы: 1). 7. ##3.7.24.1(4) Используя понятие точки разрыва функции и определения типов точек разрыва, выяснить является ли точка Ответы: 1). точка разрыва I рода 2). точка разрыва II рода 3). точка устранимого разрыва 4). нет ответа 5). не является точкой разрыва 8. ##4.2.19.1(1) Найти производную функции Ответы: 1). 9. ##4.7.18.1(1) Найти производную Ответы: 1). 10. ##5.8.15.1(1) Найти Ответы: 1). 11. ##3.5.36.2(5) Вычислить предел функции Ответы: 1). –2 2). 0 3). 1/2 4). 1 5). 12. ##4.3.28.2(2) Найти производную функции Ответы: 1). 13. ##4.11.20.2(5) Функция Ответы: 1). 14. ##5.5.26.2(4) Дана функция Ответы: 1). 15. ##5.7.14.2(2) Найти полную производную сложной функции Ответы: 1).
Департамент образования и науки Тюменской области
|

 прямые
прямые  и
и  перпендикулярны
перпендикулярны 2).
2).  3).
3). 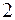 4).
4).  5).
5). 
 в точке
в точке 
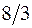 2).
2). 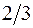 3).
3).  4).
4).  5).
5). 
 функции
функции 
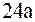 2).
2).  3).
3).  4).
4).  5).
5). 
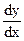 , если
, если  .
. 2). нет правильного ответа 3).
2). нет правильного ответа 3).  4).
4). 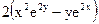 5).
5). 
 если известно, что
если известно, что  ,
, 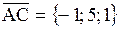 ,
,  .
. 2). нет правильного ответа 3).
2). нет правильного ответа 3). 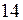 4).
4).  5).
5). 
 ,
,  параллельно оси
параллельно оси 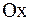
 2).
2).  3).
3). 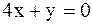 4).
4).  5).
5). 
 и проходит через точку
и проходит через точку  .
.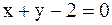 2).
2). 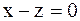 3).
3).  4).
4).  5).
5). 

 5). 1
5). 1 , при которых функция
, при которых функция 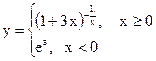 будет непрерывна в указанной точке
будет непрерывна в указанной точке  :
: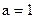 2). таких значений нет 3).
2). таких значений нет 3).  4).
4). 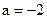 5).
5). 

 2).
2).  3).
3).  5).
5). 
 . Найти
. Найти  .
. 2).
2).  3).
3).  4).
4).  5).
5). 
 , если
, если  ,
, 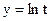 ,
, 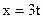 .
. 2).
2).  3). нет правильного ответа 4).
3). нет правильного ответа 4). 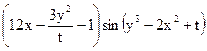 5).
5). 
 имеет вид
имеет вид 2).
2).  4).
4).  и
и 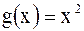 условиям теоремы Коши на отрезке
условиям теоремы Коши на отрезке  ? Если да, то указать
? Если да, то указать 
 2). Нет 3). Да,
2). Нет 3). Да, 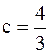 4). Да,
4). Да, 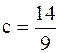 5). Да,
5). Да, 
 равен…
равен… 2).
2).  3). нет правильного ответа 4).
3). нет правильного ответа 4).  5).
5). 
 :
:  ,
, 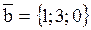 ,
, 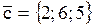
 2).
2).  3). нет правильного ответа 4).
3). нет правильного ответа 4).  5).
5). 
 :
:  ,
,  ,
,  . Составить канонические уравнения медианы
. Составить канонические уравнения медианы 
 2).
2). 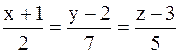 3).
3).  4).
4). 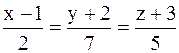 5).
5). 
 в точке
в точке 
 2).
2).  3).
3).  4).
4). 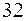 5).
5). 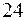
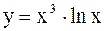
 2).
2).  3).
3). 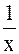 4).
4).  5).
5). 

 3). система уравнений несовместна 4).
3). система уравнений несовместна 4).  5).
5). 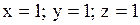
 будет непрерывна в указанной точке
будет непрерывна в указанной точке  3).
3).  4).
4).  в точке
в точке 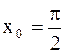 равно ….
равно …. 2).
2).  3).
3).  5).
5). 
 . Найти
. Найти  .
. 2).
2).  3).
3).  4).
4).  5).
5). 
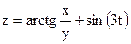 ,
,  ,
,  .
. 3).
3). 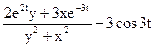 4).
4).  5).
5). 
 и
и  есть величина постоянная, равная 10
есть величина постоянная, равная 10 2).
2). 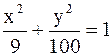 3).
3).  4).
4).  5).
5). 
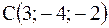 на плоскость, проходящую через параллельные прямые
на плоскость, проходящую через параллельные прямые  ,
, 
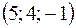 2).
2). 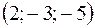 3).
3).  4).
4).  5).
5). 
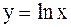 условиям теоремы Лагранжа на отрезке
условиям теоремы Лагранжа на отрезке  ? Если да, то указать
? Если да, то указать  2). Нет 3). Да,
2). Нет 3). Да,  4). Да,
4). Да,  5). Да,
5). Да, 

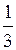 2).
2).  3).
3).  4).
4). 
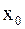 функция
функция 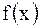 дважды непрерывно дифференцируема, и
дважды непрерывно дифференцируема, и  2).
2).  не существует 3).
не существует 3).  4).
4).  5).
5). 
 ,
, 
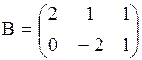 . Запишите элементы второй строки матрицы
. Запишите элементы второй строки матрицы  .
. 2).
2).  3). все предложенные ответы неверны 4).
3). все предложенные ответы неверны 4).  5).
5). 
 элемента
элемента  определителя матрицы А называется…
определителя матрицы А называется…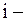 го столбца и
го столбца и 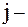 ой строки 2). определитель, полученный вычеркиванием
ой строки 2). определитель, полученный вычеркиванием 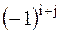 3). матрица, полученная из исходной вычеркиванием
3). матрица, полученная из исходной вычеркиванием  и
и  .
. 2). нет правильного ответа 3).
2). нет правильного ответа 3). 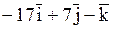 4).
4). 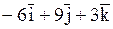 5).
5). 
 и образующей с осью
и образующей с осью  .
. 2).
2). 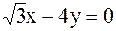 3).
3).  4).
4). 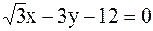 5).
5). 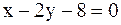
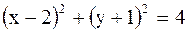 определяет
определяет до плоскости
до плоскости  вычисляется по формуле
вычисляется по формуле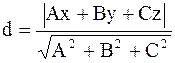 2).
2).  3).
3).  4).
4).  5).
5). 
 точкой разрыва данной функции
точкой разрыва данной функции  (в случае утвердительного ответа определить тип разрыва).
(в случае утвердительного ответа определить тип разрыва).
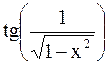 2).
2).  3).
3).  4).
4).  5).
5). 
 функции
функции 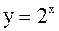
 3).
3). 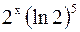 4).
4).  5).
5). 
 , если
, если  .
. 2).
2).  3).
3).  4). нет правильного ответа 5).
4). нет правильного ответа 5). 

 возрастает в интервале
возрастает в интервале 2).
2). 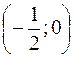 3).
3).  4).
4).  5).
5). 
 . Вычислить производную
. Вычислить производную  .
. 2). нет правильного ответа 3).
2). нет правильного ответа 3).  4).
4).  5).
5). 
 , где
, где 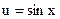 ,
,  .
. 2).
2). 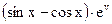 3). нет правильного ответа 4).
3). нет правильного ответа 4).  5).
5). 



