Пример круговой (секторальной) диаграммы
Часто для выражения величины сравниваемых явлений используют диаграммы, представленные в виде правильных геометрических фигур (квадратов или кругов), площадь которых пропорциональна величинам показателей. [kgl] [gl]Тема 5. Средние величины и показатели вариации[:] Цель занятия:Научиться принципам построения средних величин. Узнать их значение, виды, формы, способы расчета и применение в социально-экономических исследованиях. Структура лекции:Виды, формы, способы вычисления и использование для характеристики статистических совокупностей. Значение и определение средних величин. Значение средней величины в статистике. Средняя величина является самым распространенным обобщающим показателем в статистике. Это связано с тем, что с ее помощью можно охарактеризовать совокупность по количественно варьирующему признаку. Например, для сравнения заработной платы рабочих двух предприятий не может быть взята заработная плата двух конкретных рабочих, поскольку она выступает варьирующим показателем. Также не может быть взята общая сумма заработной платы, выплаченной на предприятиях, так как она зависит от количества работающих. Если же мы разделим общую сумму заработной платы каждого предприятия на численность работающих, то сможем их сравнить и определить, на каком предприятии средняя заработная плата выше. Иными словами заработная плата изучаемой совокупности рабочих получает обобщенную характеристику в средней величине. В ней выражается то общее и типичное, что характерно для совокупности рабочих в отношении изучаемого признака. Она в одной величине показывает общую меру этого признака, имеющего различное значение у единиц совокупности.
Определение средней величины. Средней величиной в статистике называется обобщенная характеристика совокупности однотипных явлений по какому-либо количественно варьирующему признаку. Средняя величина показывает уровень этого признака, отнесенный к единице совокупности. С помощью средней величины можно сравнивать между собой различные совокупности по варьирующим признакам (доходы на душу населения, урожайность сельскохозяйственных культур, себестоимость производства продукции на различных предприятиях). Виды средних величин. Средние величины, применяемые в статистике, относятся к классу степенных средних, общая формула которых имеет следующий вид:
,
где степенная средняя;
x – меняющиеся величины признака (варианты); n – число вариант; m – показатель степени средней; S – знак суммирования.
В статистике правильную характеристику совокупности в каждом отдельном случае дает только вполне определенный вид средних величин. Для определения этого вида средней величины используется критерий, определяющий свойства средней: средняя величина только тогда будет верной обобщающей характеристикой совокупности по варьирующему признаку, когда при замене всех вариант средней величиной общий объем варьирующего признака остается неизменным.То есть правильный вид средней определяется тем, как образуется общий объем варьирующего признака. Так, средняя арифметическая применяется тогда, когда объем варьирующего признака образуется как суммаотдельных вариант, средняя квадратическая – когда объем варьирующего признака образуется как сумма квадратов, средняя гармоническая – как сумма обратных значений отдельных вариант, средняя геометрическая – как произведениеотдельных вариант.
средняя арифметическая,
средняя гармоническая,
средняя геометрическая, где П – знак произведения. средняя квадратическая и др. (кубическая),
Все они являются частными случаями общего вида средних (степенных):
х - меняющиеся значения признака (варианты); п - число вариант (наблюдений); m – показатель степени средней.
Если варианты встречаются часто, то эти средние могут быть исчислены с учетом частоты встречающихся вариант и называются средними взвешенными, если нет, то средними простыми. Из этих видов средних степенных в статистике наиболее часто применяются средние арифметические, реже – средние гармонические (в силу наличия соответствующих исходных данных), при расчете средних темпов роста (динамики) используется средняя геометрическая, а средняя квадратическая – при расчете показателей вариации.
|




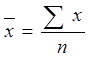 ;
;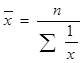 ;
; ;
;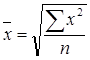 .
.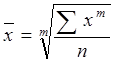 , где
, где 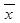 - средняя;
- средняя;


