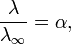Закон разбавления Оствальда — соотношение, выражающее зависимость эквивалентной электропроводности разбавленного раствора бинарного слабого электролита от концентрации раствора:

Здесь К — константа диссоциации электролита, с — концентрация, λ и λ∞ — значения эквивалентной электропроводности соответственно при концентрации с и при бесконечном разбавлении. Соотношение является следствием закона действующих масс и равенства
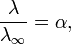
где α — степень диссоциации.
Закон разбавления Оствальда выведен В.Оствальдом в 1888 и им же подтвержден опытным путём. Экспериментальное установление правильности закона разбавления Оствальда имело большое значение для обоснования теории электролитической диссоциации.
Процесс распада полярного вещества в растворе на ионы называют электролитической диссоциацией (ионного – ионизацией). По способности к электролитической диссоциации электролиты обычно подразделяют на сильные и слабые. К сильным электролитам обычно относят вещества, которые в растворе практически полностью диссоциированы на ионы. Слабыми электролитами считают вещества, степень диссоциации, которых невелика. Понятие степень диссоциации электролита α как величины, равной отношению числа распавшихся (диссоциированных) молекул Nдисс к общему числу молекул N0 электролита, α = Nдисс /Nо было введено Аррениусом – создателем первой количественной теории растворов электролитов. Теория электролитической диссоциации и основанная на ней классификация кислот и оснований в полной мере применимы лишь к водным растворам.
Процесс электролитической диссоциации возникающий в результате сольватации, обратим, т.е. наряду с равпадом молекул растворенного вещества происходит их образование из ионов:
Кm Аn D mКZ1+ + nАZ2- где Кm Аn – молекула электролита; КZ1+- катион; АZ2- - анион; Z1 и Z2 - заряд аниона и катиона соответственно; n и m – стехиометрические коэффициенты. Равновесие между ионами и молекулами электролита подчиняется закону действия масс. Поэтому важной характеристикой процесса диссоциации является константа диссоциации (константа ионизации) Кd (С), вычисленная по равновесным концентрациям молекул и ионов: Кd (С) = [КZ1+] m [АZ2-]n ⁄[К mАn], где [КZ1+], [АZ2-] –равновесные молярные концентрации катионов и анионов соответственно; [К mАn] - равновесная молярная концентрация недиссоциированных молекул электролита.
Константу равновесия процесса диссоциации принято обозначать Ка в случае слабых кислот и Кb для слабых оснований.
Пример диссоциации слабого основания (гидроксид аммония) NН4ОН D NН4+ + ОН-
Кb = [NН4+] [ОН-] /[NН4ОН] = 1,8 ×10-5
Многоосновные кислоты и многоосновные основания диссоциируют ступенчато.
Константа диссоциации характеризует процесс диссоциации данного электролита в данном растворителе, но не зависит от концентрации электролита и при постоянной температуре Кd (С) =соnst. Очевидно, что степень диссоциации α тем больше, чем ниже концентрация, т.е. чем сильнее разбавлен раствор.
В состоянии равновесия концентрации катионов КZ+ и анионов АZ- будут равны [КZ+] = [АZ-] = α С, а концентрация недиссоциированных молекул [КА] = (С – α С) = С (1- α) подставляя эти выражения в уравнение для константы диссоциации получим:
Кd (С) = α2 × С
1- α -это выражение описывает закон разбавления (разведения) Оствальда для слабых электролитов. В случае когда степень диссоциации электролита α<<1, что имеет место при С /Кd (С) >100, величиной α по сравнению с 1 можно пренебречь и закон разбавления Оствальда записать в упрощенном варианте Кd (С) = α2С.
Из закона разбавления Оствальда следует, что степень диссоциации уменьшается с увеличением концентрации слабого электролита.