На практике свободные незатухающие колебания получить невозможно, так как часть энергии тратится на выделение тепла в проводниках и излучение в пространство электромагнитных волн за пределами конденсатора и катушки индуктивности. В этих случаях колебания являются затухающими.
Уравнение затухающих колебаний получим на основе второго правила Кирхгофа с учетом напряжений на активном сопротивлении  и на конденсаторе
и на конденсаторе 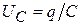 (рис. 2)
(рис. 2)

 . (4)
. (4)
Преобразуем уравнение (4) к виду
 (5)
(5)
и, используя обозначения  ,
, 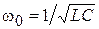 , получим
, получим
 . (6)
. (6)
Решением дифференциального уравнения затухающих колебаний (6) при
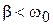 является выражение
является выражение
 , (7)
, (7)
где q 0 – начальная амплитуда колебаний заряда,  – циклическая частота собственных затухающих колебаний,
– циклическая частота собственных затухающих колебаний,  – начальная фаза колебаний, определяемая из начальных условий. Зависимость q (t) показана на рис. 3. Качественно такие же зависимости характеризуют затухающие колебания напряжения на конденсаторе (U = q / C) и силы тока I.
– начальная фаза колебаний, определяемая из начальных условий. Зависимость q (t) показана на рис. 3. Качественно такие же зависимости характеризуют затухающие колебания напряжения на конденсаторе (U = q / C) и силы тока I.
Частота затухающих колебаний  меньше частоты собственных незатухающих колебаний
меньше частоты собственных незатухающих колебаний  . Амплитуда затухающих колебаний уменьшается с течением времени по экспоненциальному закону
. Амплитуда затухающих колебаний уменьшается с течением времени по экспоненциальному закону  (рис. 3). Коэффициент затухания
(рис. 3). Коэффициент затухания  показывает, во сколько раз уменьшается амплитуда колебаний за единицу времени. Величина
показывает, во сколько раз уменьшается амплитуда колебаний за единицу времени. Величина 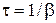 называется временем релаксации. За время
называется временем релаксации. За время  амплитуда затухающих колебаний уменьшается в e раз.
амплитуда затухающих колебаний уменьшается в e раз.
 Величина, равная натуральному логарифму отношения амплитуд колебаний для двух последовательных моментов времени t и t + T, отличающихся на период, называется логарифмическим декрементом затухания
Величина, равная натуральному логарифму отношения амплитуд колебаний для двух последовательных моментов времени t и t + T, отличающихся на период, называется логарифмическим декрементом затухания  . Подстановка выражения для амплитуды колебаний дает связь с коэффициентом затухания
. Подстановка выражения для амплитуды колебаний дает связь с коэффициентом затухания  и временем релаксации:
и временем релаксации:  . Логарифмический декремент затухания
. Логарифмический декремент затухания 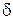 характеризует уменьшение амплитуды колебания за один период. В соответствии с определением
характеризует уменьшение амплитуды колебания за один период. В соответствии с определением  , логарифмический декремент затухания есть величина, обратная числу колебаний, за которые амплитуда убывает в е раз.
, логарифмический декремент затухания есть величина, обратная числу колебаний, за которые амплитуда убывает в е раз.
С логарифмическим декрементом затухания связана добротность Q, которая определяется через отношение энергии, запасённой в контуре W (t), к энергии  , теряемой за период. А поскольку энергия пропорциональна квадрату амплитуды колебаний, то добротность выражается следующим образом:
, теряемой за период. А поскольку энергия пропорциональна квадрату амплитуды колебаний, то добротность выражается следующим образом:
 . (8)
. (8)
При малом затухании  или
или  . Чем выше добротность контура, тем больше колебаний совершается за время
. Чем выше добротность контура, тем больше колебаний совершается за время  .
.
1.3. Вынужденные колебания
Для того чтобы в контуре, где есть потери энергии, создать незатухающие колебания, можно включить в контур источник тока с переменной ЭДС  . Колебания, возникающие под действием внешнего гармонического воздействия, называются вынужденными колебаниями (рис. 4).
. Колебания, возникающие под действием внешнего гармонического воздействия, называются вынужденными колебаниями (рис. 4).
При последовательном включении источника тока в цепь в уравнении (4), записанном для замкнутого контура, необходимо учесть ЭДС источника:

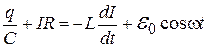 . (9)
. (9)
Уравнение (9) приведем к виду
 , (10)
, (10)  , (11)
, (11)
где использованы прежние обозначения:  ,
, 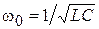 . Решением дифференциального уравнения вынужденных колебаний (11) является уравнение гармонического колебания, которое происходит с частотой, равной частоте колебаний ЭДС внешнего источника:
. Решением дифференциального уравнения вынужденных колебаний (11) является уравнение гармонического колебания, которое происходит с частотой, равной частоте колебаний ЭДС внешнего источника:
 , (12)
, (12)
но отличается от него по фазе. Сдвиг фазы определяется по формуле
 . (13)
. (13)
Амплитуда вынужденных установившихся колебаний заряда зависит от частоты  (рис. 5 а),
(рис. 5 а),  и параметров контура
и параметров контура
 . (14)
. (14)
Аналогичную зависимость от частоты  имеет амплитуда колебаний напряжения (рис. 5 а).
имеет амплитуда колебаний напряжения (рис. 5 а).

 и на конденсаторе
и на конденсаторе 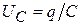 (рис. 2)
(рис. 2)
 . (4)
. (4) (5)
(5) ,
, 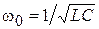 , получим
, получим . (6)
. (6)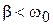 является выражение
является выражение , (7)
, (7) – циклическая частота собственных затухающих колебаний,
– циклическая частота собственных затухающих колебаний,  – начальная фаза колебаний, определяемая из начальных условий. Зависимость q (t) показана на рис. 3. Качественно такие же зависимости характеризуют затухающие колебания напряжения на конденсаторе (U = q / C) и силы тока I.
– начальная фаза колебаний, определяемая из начальных условий. Зависимость q (t) показана на рис. 3. Качественно такие же зависимости характеризуют затухающие колебания напряжения на конденсаторе (U = q / C) и силы тока I. меньше частоты собственных незатухающих колебаний
меньше частоты собственных незатухающих колебаний  . Амплитуда затухающих колебаний уменьшается с течением времени по экспоненциальному закону
. Амплитуда затухающих колебаний уменьшается с течением времени по экспоненциальному закону  (рис. 3). Коэффициент затухания
(рис. 3). Коэффициент затухания  показывает, во сколько раз уменьшается амплитуда колебаний за единицу времени. Величина
показывает, во сколько раз уменьшается амплитуда колебаний за единицу времени. Величина 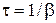 называется временем релаксации. За время
называется временем релаксации. За время  амплитуда затухающих колебаний уменьшается в e раз.
амплитуда затухающих колебаний уменьшается в e раз. Величина, равная натуральному логарифму отношения амплитуд колебаний для двух последовательных моментов времени t и t + T, отличающихся на период, называется логарифмическим декрементом затухания
Величина, равная натуральному логарифму отношения амплитуд колебаний для двух последовательных моментов времени t и t + T, отличающихся на период, называется логарифмическим декрементом затухания  . Подстановка выражения для амплитуды колебаний дает связь с коэффициентом затухания
. Подстановка выражения для амплитуды колебаний дает связь с коэффициентом затухания  . Логарифмический декремент затухания
. Логарифмический декремент затухания 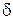 характеризует уменьшение амплитуды колебания за один период. В соответствии с определением
характеризует уменьшение амплитуды колебания за один период. В соответствии с определением  , логарифмический декремент затухания есть величина, обратная числу колебаний, за которые амплитуда убывает в е раз.
, логарифмический декремент затухания есть величина, обратная числу колебаний, за которые амплитуда убывает в е раз. , теряемой за период. А поскольку энергия пропорциональна квадрату амплитуды колебаний, то добротность выражается следующим образом:
, теряемой за период. А поскольку энергия пропорциональна квадрату амплитуды колебаний, то добротность выражается следующим образом: . (8)
. (8) или
или  . Чем выше добротность контура, тем больше колебаний совершается за время
. Чем выше добротность контура, тем больше колебаний совершается за время  .
. . Колебания, возникающие под действием внешнего гармонического воздействия, называются вынужденными колебаниями (рис. 4).
. Колебания, возникающие под действием внешнего гармонического воздействия, называются вынужденными колебаниями (рис. 4).
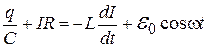 . (9)
. (9) , (10)
, (10)  , (11)
, (11) , (12)
, (12) . (13)
. (13) и параметров контура
и параметров контура . (14)
. (14)


