Формула Коши-Адамара.
Используя радикальный признак Коши и рассуждая аналогичным образом, получим, что можно задать область сходимости степенного ряда как множество решений неравенства
Теорема 2 (2-я теорема Абеля). Если R – радиус сходимости ряда Пример 1. Найти область абсолютной и равномерной сходимости ряда Решение: В этом случае для решения задачи удобно использовать радикальный признак Коши
или Исследуем поведение ряда а) б) Пример 2. Найти радиус сходимости и область абсолютной и равномерной сходимости степенного ряда Решение. Найдем радиус сходимости данного ряда этого можно применить признак Даламбера в предельной форме: Радиус сходимости – половина интервала сходимости, поэтому интервал сходимости: Исследуем поведение ряда на концах интервала сходимости: а) при
б) при Пример 3. Найти радиус сходимости и интервал сходимости ряда Решение. Для отыскания радиуса сходимости данного степенного ряда удобно воспользоваться радикальным признаком Коши в предельной форме:
тогда радиус сходимости Интервал сходимости: Исследуем поведение ряда в концевых точках интервала сходимости: а) при
б) при Пример 4. Найти радиус и область абсолютной и равномерной сходимости ряда Решение. Найдем радиус сходимости:
Центром ряда является точка
Поведение ряда в концевых точках интервала сходимости: при Итак, данный степенной ряд сходится абсолютно и равномерно для Пример 5. Найти область абсолютной и равномерной сходимости степенного ряда Решение. Здесь Пример 6. Исследовать на сходимость степенной ряд Решение. Здесь
|

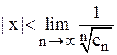 при условии существования этого предела, и, соответственно, найти еще одну формулу для радиуса сходимости:
при условии существования этого предела, и, соответственно, найти еще одну формулу для радиуса сходимости: (4)
(4) и этот ряд сходится при
и этот ряд сходится при  , то он равномерно сходится на отрезке
, то он равномерно сходится на отрезке  .
. .
. , тогда
, тогда
 , раскрывая неравенство, получим
, раскрывая неравенство, получим  или
или  .
. :
:  – знакочередующийся ряд, для которого не выполняется необходимый признак сходимости, т.е. ряд расходится;
– знакочередующийся ряд, для которого не выполняется необходимый признак сходимости, т.е. ряд расходится; :
:  – ряд расходится, т.к. для него не выполняется необходимый признак сходимости
– ряд расходится, т.к. для него не выполняется необходимый признак сходимости 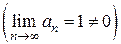 . Таким образом, для ряда
. Таким образом, для ряда 
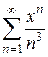 .
. , тогда радиус сходимости
, тогда радиус сходимости  .
.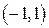 .
. :
:  . Ряд, составленный из модулей членов этого ряда,
. Ряд, составленный из модулей членов этого ряда,  сходится (как гипергармонический ряд
сходится (как гипергармонический ряд  с
с  ), следовательно, ряд
), следовательно, ряд получим ряд
получим ряд 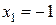 и
и  входят в область абсолютной и равномерной сходимости:
входят в область абсолютной и равномерной сходимости: 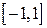 .
. .
. ,
,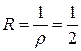 .
.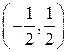 .
. :
:  это знакочередующийся числовой ряд. Этот ряд расходится, т.к. для него не выполняется признак Лейбница:
это знакочередующийся числовой ряд. Этот ряд расходится, т.к. для него не выполняется признак Лейбница:
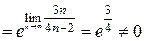 ;
; получим ряд
получим ряд  . Этот ряд тоже расходится, т.к. не выполняется необходимый признак сходимости:
. Этот ряд тоже расходится, т.к. не выполняется необходимый признак сходимости: 
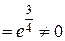 . Следовательно, в предельных точках интервала
. Следовательно, в предельных точках интервала  расходится, область сходимости этого ряда:
расходится, область сходимости этого ряда:  .
. ,
,  ,
,  .
. , Интервал сходимости
, Интервал сходимости  (рис.1).
(рис.1).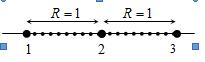
 :
:  – знакочередующийся числовой ряд, сходится абсолютно; при
– знакочередующийся числовой ряд, сходится абсолютно; при 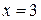 :
:  – сходится.
– сходится. .
.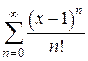 .
. ,
,  . Найдем радиус R сходимости ряда
. Найдем радиус R сходимости ряда 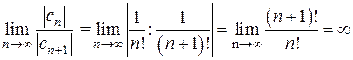 . Следовательно, область абсолютной сходимости ряда
. Следовательно, область абсолютной сходимости ряда  , область равномерной сходимости- любая ограниченная область.
, область равномерной сходимости- любая ограниченная область. .
. и
и  . Найдем радиус R сходимости ряда
. Найдем радиус R сходимости ряда 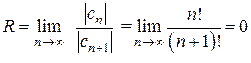 . Следовательно, область сходимости ряда состоит из одной точки
. Следовательно, область сходимости ряда состоит из одной точки 


