Теорема. Если две плоскости перпендикулярны между собой, то одна прямая одной плоскости перпендикулярна двум прямым другой плоскости.
Глоссарий
Основная литература: 1. Соколова Т.Ю. AutoCAD 2009. Учебный курс. Москва. 2008. 2. Соколов Т.Ю. AutoCAD 20010. Учебный курс. Москва 2009 3. Левковец Л.Б. AutoCAD 2011.Самоучитель. Санкт- Петербург. 2010. Дополнительная литература: 4. AutoCAD 2010. Руководство пользователя. I, II, III тома. Autodesk. 5. Жунусов А.Ш., Сейдахмет А.Ж. АРМ (тренинги) по AutoCAD 2010. Алматы, КазГАСА. Сентябрь, 2009г. Шишанов А. В.Дизайн интерьеров в 3ds Max 2011. Санкт- Петербург. 2010. 7. Жунусов А.Ш., Буганова С. Н. АРМ (тренинги) по AutoCAD 2011 и 3ds Max Design 2011. Алматы, КазАкпарат. Апрель, 2011г.
Задание на СРС 1. Начертательная геометрия в2D: Конструктивные и метрические задачи. 7(46-51). Задание на СРСП 1. Измерение расстояний, углов, площади 1(346-347).
Контрольные вопросы А. для письменного экзамена 1. Каково назначение команды Multiline? 2. Каково назначение опции Break? 3. Можно ли разметить объект блоком? Б. Тестовые задания для контрольного тестирования 1. Назначение команды «Угловой» в нанесении размера: A. Нанесение углового размера B. Нанесение выровненного размера C. Нанесение радиального размера D. Нанесение диаметрального размера 2. С помощью какой команды можно изменить цвет граней? A. Редактирование – Изменить цвет граней; B. Редактирование – Выдавить грани; C. Редактирование – Повернуть грани; D. Редактирование – Удалить грани; 3. Назначение команды диаметр: A. Нанесение диаметрального размера B. Нанесение углового размера C. Нанесение радиального размера D. Нанесение выровненного размера 4. Назначение команды линейный: A. Нанесение линейного размера B. Нанесение углового размера C. Нанесение радиального размера D. Нанесение выровненного размера 5. Назначение команды радиус: A. Нанесение радиального размера B. Нанесение углового размера C. Нанесение линейного размера D. Нанесение выровненного размера
Глоссарий
Основная литература: 1. Соколова Т.Ю. AutoCAD 2009. Учебный курс. Москва. 2008. 2. Соколов Т.Ю. AutoCAD 20010. Учебный курс. Москва 2009 3. Левковец Л.Б. AutoCAD 2011.Самоучитель. Санкт- Петербург. 2010. Дополнительная литература: 4. AutoCAD 2010. Руководство пользователя. I, II, III тома. Autodesk. 5. Жунусов А.Ш., Сейдахмет А.Ж. АРМ (тренинги) по AutoCAD 2010. Алматы, КазГАСА. Сентябрь, 2009г. Шишанов А. В.Дизайн интерьеров в 3ds Max 2011. Санкт- Петербург. 2010. 7. Жунусов А.Ш., Буганова С. Н. АРМ (тренинги) по AutoCAD 2011 и 3ds Max Design 2011. Алматы, КазАкпарат. Апрель, 2011г.
Теорема. Если две плоскости перпендикулярны между собой, то одна прямая одной плоскости перпендикулярна двум прямым другой плоскости. В качестве одной прямой заданной плоскости можно взять любую сторону треугольника (например AС). В качестве двух прямых конструируемой плоскости можно взять её горизонталь h1 и фронталь f1. Проведем (

Новая плоскость (h1 f1) перпендикулярна заданной плоскости ABC, так как две прямые (h1 и f1) перпендикулярны прямой AС. 3. Найдем расстояние от точки D до плоскости ABC. Чтобы решить задачу опустим перпендикулярную к плоскости прямую ДК, проходящую через точку D, построим пересечение этого перпендикуляра с плоскостью ABC в точке К, затем определим натуральную величину отрезка DК. Теорема. Если прямая перпендикулярна плоскости,то фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (D1 K1 ┴ f1), а горизонтальная проекция – горизонтальной проекции горизонтали плоскости (D2 K2 ┴ h2).

Для нахождения точки К (К1,К2),построим плоскость сечения, проходящую через направления DK и находим пересечение 5,6,затем точку К как пересечение этой линии с перпендикуляром. Для этого включим объектную привязку


Для нахождения натуральной величины отрезка DK, используем меню «Параметризация», которое появилось в последней версии Auto CAD 2010:


Построена натуральная величина (K1D) расстояния от точки D до плоскости ABC. Сохраним чертёж под именем «АРМ № 16 Расстояние от точки D до плоскости ABC» или продолжим АРМ №17.
|

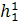 ║h;
║h;  ┴ A1 С1) и (
┴ A1 С1) и ( ┴ A2 С2 ;
┴ A2 С2 ;  ║f2), для чего включим объектные привязки: «конточка» и
║f2), для чего включим объектные привязки: «конточка» и 
 )>EE(построена f12)
)>EE(построена f12)
 > точка D1> орто> провести
> точка D1> орто> провести  >EE
>EE
 > указать f1 (31, 41 )(появится значок
> указать f1 (31, 41 )(появится значок  (если отключена), затем:
(если отключена), затем: > Орто> K2> вправо до точки D(появится привязка
> Орто> K2> вправо до точки D(появится привязка  > K1> D> EE (K 1 D-натуральная величина отрезка).
> K1> D> EE (K 1 D-натуральная величина отрезка).




