Задание 1. Определение коэффициента жесткости пружины статическим методом
1. С помощью крепежного винта подвесьте пружину вертикально к горизонтальному стержню. К пружине уже прикреплен небольшой груз. Получившаяся конструкция представляет собой пружинный маятник. 2. На стенде напротив пружины установите линейку – она понадобится для определения удлинений пружины в ходе работы. Зафиксируйте координату нижней плоскости груза в положении равновесия – от этой точки далее будет производиться отсчет координаты x. 3. Произведите последовательно измерения координаты x относительно начального положения для пяти различных масс. 4. Считая условием равновесия mg = kx, постройте график зависимости mg (x) (значение ускорения свободного падения g принимайте равным 9.81 м/с2 без погрешности). Если деформации пружины упругие, т. е. после прекращения действия силы пружина восстанавливает первоначальные геометрические параметры (на практике это условие выполняется при малых удлинениях пружины), то закон Гука справедлив (k = const) и график будет линейным. Тангенс угла наклона полученной прямой дает среднее значение коэффициента жесткости k. Для произвольной точки прямой 5. Погрешностью отдельного прямого измерения величин, отложенных на осях, считают отклонение экспериментального значения рассматриваемой величины от значения, даваемого графиком. Установив таким образом относительные погрешности всех отдельных прямых измерений m и x, усредните их по пяти измерениям. Значит, погрешность k будет определяться выражениями 6. Данные желательно упорядочить в виде таблицы:
7. Представьте конечный результат:
|

 .
. ,
,  .
.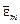
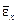
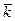 , н/м
, н/м
 ,
,  .
.


