Совместные и противоположенные обстоятельства.
Если два обстоятельства А и В могут существовать одновременно, то такие обстоятельства будут называться совместными, в противном случае – несовместными. Тем самым, А и Если из актуального существования некоторого обстоятельства А с необходимостью следует актуальное существование другого обстоятельства В, то А будем называть достаточной причиной или основанием В и обозначать Можно также рассмотреть и иные случаи соотношения обстоятельств А, В и противоположенных им, представленные в таблице 2.1 (цифрой 1 отмечено отношение, при котором из существования одного обстоятельства с необходимостью следует существование другого). Очевидно, что эта цифра не может повторяться в строке дважды – так как В и
Таблица 2.1. Отношение двух обстоятельств.
Если У одного и того же обстоятельства может существовать несколько необходимых, причин, причем из существования следствия можно сделать вывод о совместности этих причин. Множество всех необходимых причин для некоторого обстоятельства В будем обозначать Утверждение 2. Пусть Действительно, если Если существует некоторое обстоятельство А, то множество всех обстоятельств В1, В2, … для которых Утверждение 3. Пусть Утверждение 4. Пусть Пример 2.1. Примером результата является претерпевание действия.
|

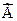 – несовместные обстоятельства.
– несовместные обстоятельства. . Если из актуального несуществования А с необходимостью следует актуальное несуществование В, то А будем называть необходимой причиной В и обозначать
. Если из актуального несуществования А с необходимостью следует актуальное несуществование В, то А будем называть необходимой причиной В и обозначать 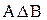 . Обстоятельство В будем называть следствием А.
. Обстоятельство В будем называть следствием А. несовместны.
несовместны.

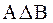



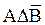

 и
и  . Для них по существованию А можно сделать вывод о существовании В и наоборот.
. Для них по существованию А можно сделать вывод о существовании В и наоборот.
 ~
~ 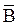
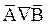 . Действительно, если А необходимая причина В, то из отсутствия А, т.е.
. Действительно, если А необходимая причина В, то из отсутствия А, т.е.  ) или иначе
) или иначе  . Аналогично, множество всех достаточных причин (оснований) для существования В будем обозначать
. Аналогично, множество всех достаточных причин (оснований) для существования В будем обозначать 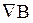 .
. ,
,  и A1 несовместно с A2. Тогда
и A1 несовместно с A2. Тогда  , т.е. для него нет необходимых причин.
, т.е. для него нет необходимых причин. , то
, то 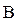 будет существовать только при существовании А1, а следовательно А2 не может быть необходимой причиной В, если они существовать одновременно не могут. Аналогично показывается для А2. Любое иное обстоятельство А не может быть необходимой причиной, так как при допущении противного А1 (или А2) не были бы достаточной причиной В.
будет существовать только при существовании А1, а следовательно А2 не может быть необходимой причиной В, если они существовать одновременно не могут. Аналогично показывается для А2. Любое иное обстоятельство А не может быть необходимой причиной, так как при допущении противного А1 (или А2) не были бы достаточной причиной В. обозначается
обозначается 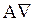 и следствия В n будем называть результатами А.
и следствия В n будем называть результатами А.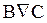 . Тогда
. Тогда  .
. и
и  . Тогда
. Тогда  .
.


