Упражнение 1
1. Измерить диаметр 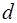 проволоки подвеса и диаметры
проволоки подвеса и диаметры  и
и  дисков (штангенциркулем) и длину подвеса (линей-кой).
дисков (штангенциркулем) и длину подвеса (линей-кой).
2. Измерить время 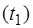
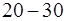 колебаний маятника, по-вернув диск приблизительно на 30°. Провести не менее пя-ти таких наблюдений, результаты занести в таблицу 1.
колебаний маятника, по-вернув диск приблизительно на 30°. Провести не менее пя-ти таких наблюдений, результаты занести в таблицу 1.
3. Измерить время 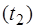
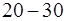 колебаний маятника с дву-мя дисками. Провести также не менее пяти экспериментов и результаты занести в таблицу 1.
колебаний маятника с дву-мя дисками. Провести также не менее пяти экспериментов и результаты занести в таблицу 1.
Таблица 1
| № опыта
|  1, сек 1, сек
| 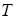 1, сек 1, сек
| t2, сек
| T2, сек
|
|
|
|
| t
|
|
| ...
|
|
|
|
|
|
|
|
|
|
|
| среднее
|
|
|
|
|
4. По данным п.п. 2, 3 вычислить периоды колебаний маятника с одним (T1) и с двумя (T2) дисками. Определить погрешность с доверительной вероятностью 90%:
 ,
,
где  – средняя квадратичная ошибка (для T2 аналогично
– средняя квадратичная ошибка (для T2 аналогично 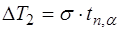 ).
).
5. Рассчитать относительные ошибки
 и
и 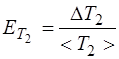 .
.
Упражнение 2
5. Измерить время затухания колебаний маятника  , за которое амплитуда
, за которое амплитуда  колебаний уменьшится примерно вдвое, повернув изначально диск приблизительно на 30°(
колебаний уменьшится примерно вдвое, повернув изначально диск приблизительно на 30°( ). Про-вести не менее пяти экспериментов результаты занести в таблицу 2.
). Про-вести не менее пяти экспериментов результаты занести в таблицу 2.
Таблица 2
| № опыта
|  , град , град
| 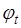 , град , град
|  , сек , сек
|
|
|
|
|
|
| ...
|
|
|
|
|
|
|
|
|
| среднее
|
|
|
|
6. По данным п. 5 вычислить постоянную времени зату-хания маятника  и погрешность
и погрешность  с доверительной ве-роятностью 90%.
с доверительной ве-роятностью 90%.
Так как отклонение маятника отсчитывается от некото-рого нулевого положения ( ) (в общем случае отличного от нуля), то закон убывания амплитуды колебаний в со-ответствии с (2.9) имеет вид:
) (в общем случае отличного от нуля), то закон убывания амплитуды колебаний в со-ответствии с (2.9) имеет вид:
 ,
,
 . (2.19)
. (2.19)
7. Измерения и вычисления по пп. 5,6 повторить для маятника с двумя дисками.
8. Оценить относительный сдвиг частоты (и периода)  , обусловленный затуханием колебаний (трением). Следует отметить, что при малом затухании:
, обусловленный затуханием колебаний (трением). Следует отметить, что при малом затухании:
 ,
,
поэтому согласно формуле (2.11):
 ,
,
откуда
 , (2.20)
, (2.20)
где  .
.
9. Определить момент инерции ( ) маятника из соотно-шения частот для маятника с одним и двумя дисками. На основании (2.5) имеем:
) маятника из соотно-шения частот для маятника с одним и двумя дисками. На основании (2.5) имеем:
 (2.21)
(2.21)
где  – момент инерции второго диска, добав-ляемый к моменту инерции крутильного маятника. Если по п. 8 разница между
– момент инерции второго диска, добав-ляемый к моменту инерции крутильного маятника. Если по п. 8 разница между  и
и  оказывается пренебрежительно малой, то
оказывается пренебрежительно малой, то  можно заменить на
можно заменить на  , тогда расчетная формула (2.21) примет вид
, тогда расчетная формула (2.21) примет вид
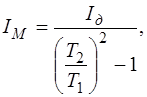 (2.22)
(2.22)
где  и
и  определены в п. 4.
определены в п. 4.
10. Найти относительную ошибку  момента инерции маятника по формуле:
момента инерции маятника по формуле:
 ,
,
где  и
и  – систематические ошибки
– систематические ошибки  и
и  . Если какое-либо из слагаемых гораздо больше остальных, будет разумно при вычислениях оставлять только его.
. Если какое-либо из слагаемых гораздо больше остальных, будет разумно при вычислениях оставлять только его.
11. Рассчитайте абсолютную ошибку
 .
.
12. Определить коэффициент кручения  по формуле (2.6), используя найденные значения момента инерции маятника
по формуле (2.6), используя найденные значения момента инерции маятника  в п. 9 (2.22) и периода
в п. 9 (2.22) и периода  в п.4.
в п.4.
13. Рассчитать относительную ошибку  по формуле:
по формуле:
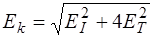 ,
,
где  и
и 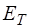 – относительные ошибки момента инерции ма-ятника
– относительные ошибки момента инерции ма-ятника  и периода и абсолютную ошибку
и периода и абсолютную ошибку  . Результат представить в стандартном виде и округлить с нужной степенью точности.
. Результат представить в стандартном виде и округлить с нужной степенью точности.
14. Используя найденные значения постоянной времени затухания в п. 6 и момента инерции маятника в п. 9, можно вычислить обобщенный коэффициент сопротивления  по формуле (2.10).
по формуле (2.10).

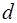 проволоки подвеса и диаметры
проволоки подвеса и диаметры  и
и  дисков (штангенциркулем) и длину подвеса (линей-кой).
дисков (штангенциркулем) и длину подвеса (линей-кой).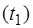
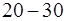 колебаний маятника, по-вернув диск приблизительно на 30°. Провести не менее пя-ти таких наблюдений, результаты занести в таблицу 1.
колебаний маятника, по-вернув диск приблизительно на 30°. Провести не менее пя-ти таких наблюдений, результаты занести в таблицу 1.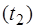
 1, сек
1, сек
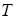 1, сек
1, сек
 ,
, – средняя квадратичная ошибка (для T2 аналогично
– средняя квадратичная ошибка (для T2 аналогично 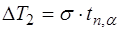 ).
). и
и 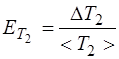 .
. , за которое амплитуда
, за которое амплитуда  колебаний уменьшится примерно вдвое, повернув изначально диск приблизительно на 30°(
колебаний уменьшится примерно вдвое, повернув изначально диск приблизительно на 30°( ). Про-вести не менее пяти экспериментов результаты занести в таблицу 2.
). Про-вести не менее пяти экспериментов результаты занести в таблицу 2. , град
, град
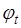 , град
, град
 , сек
, сек
 и погрешность
и погрешность  с доверительной ве-роятностью 90%.
с доверительной ве-роятностью 90%. ) (в общем случае отличного от нуля), то закон убывания амплитуды колебаний в со-ответствии с (2.9) имеет вид:
) (в общем случае отличного от нуля), то закон убывания амплитуды колебаний в со-ответствии с (2.9) имеет вид: ,
, . (2.19)
. (2.19) , обусловленный затуханием колебаний (трением). Следует отметить, что при малом затухании:
, обусловленный затуханием колебаний (трением). Следует отметить, что при малом затухании: ,
, ,
, , (2.20)
, (2.20) .
. ) маятника из соотно-шения частот для маятника с одним и двумя дисками. На основании (2.5) имеем:
) маятника из соотно-шения частот для маятника с одним и двумя дисками. На основании (2.5) имеем: (2.21)
(2.21) – момент инерции второго диска, добав-ляемый к моменту инерции крутильного маятника. Если по п. 8 разница между
– момент инерции второго диска, добав-ляемый к моменту инерции крутильного маятника. Если по п. 8 разница между  и
и  оказывается пренебрежительно малой, то
оказывается пренебрежительно малой, то 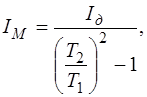 (2.22)
(2.22) и
и  определены в п. 4.
определены в п. 4. момента инерции маятника по формуле:
момента инерции маятника по формуле: ,
, и
и  – систематические ошибки
– систематические ошибки  и
и  .
. по формуле (2.6), используя найденные значения момента инерции маятника
по формуле (2.6), используя найденные значения момента инерции маятника 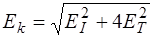 ,
,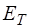 – относительные ошибки момента инерции ма-ятника
– относительные ошибки момента инерции ма-ятника  . Результат представить в стандартном виде и округлить с нужной степенью точности.
. Результат представить в стандартном виде и округлить с нужной степенью точности. по формуле (2.10).
по формуле (2.10).


