МЕТОДИЧЕСКИЕ И ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ. Различают три основных вида волн: упругие (звуковые, сейсмические и т.д.), электромагнитные (свет, радиоволны и др.) и волны на поверхности жидкости.
Различают три основных вида волн: упругие (звуковые, сейсмические и т.д.), электромагнитные (свет, радиоволны и др.) и волны на поверхности жидкости. Поверхностные волны выделены в отдельную группу, т.к., по словам Р.Фейнмана, "...эти волны нисколько не похожи ни на звук, ни на свет, здесь собраны все трудности, какие могут быть в волнах." Действительно, поскольку модуль сдвига для жидкостей и газов равен нулю, то поперечные волны в этих средах распространяться не могут. Вместе с тем, если следить лишь за изменениями положения поверхностного слоя жид-кости, подвергнутой возмущению, то волны на её поверх-ности можно назвать поперечными. При формировании волн на поверхности рек и различных водоемов сочетание раз-личных физических процессов бывает настолько трудно учи-тываемым (плюс ко всему еще и эффект удара при прибли-жении к берегу), что, например, процесс возникновения хо-рошо известной из наблюдений изогнутой волны до настоя-щего времени не описан. Вместе с тем, изучение поверх-ностных волн имеет большое практическое значение для су-достроения, при проектировании и эксплуатации гидросамо-летов и т.д. Ниже рассматриваются идеализированные усло-вия формирования поверхностных волн в лабораторных усло-виях, когда ванна заполняется водой, вязкость которой пола-гается пренебрежимо малой, а источником возмущающей силы является погруженный в воду на 0,5 – 1 мм вибратор, совершающий возвратно-поступательное колебательное дви-жение. При возникновении волновых колебательных процессов кроме возмущающей должна существовать и возвращающая сила. В случае поверхностных волн роль возвращающей силы играют силы поверхностного натяжения и силы тяжести. Поверхность покоящейся жидкости, находящейся под воз-действием только силы тяжести, горизонтальна. Всякое искрив-ление поверхности жидкости, вызванное действием возму-щающей силы (колебания вибратора), связано с увеличением её потенциальной энергии, обусловленной действием сил по-верхностного натяжения. Под действием этих сил поверх-ность стремится уменьшиться, т.е. возвратиться в горизон-тальное положение, в котором потенциальная энергия мини-мальна. При небольших амплитудах волн пути отдельных частиц жидкости с некоторым (довольно большим) приближе-нием можно считать окружностями. Круговое движение час-тиц возникает в связи с тем, что имеет место сумма про-дольных и поперечных волн. Диаметры этих круговых путей наибольшие для частиц, находящихся на поверхности, и быс-тро уменьшаются с глубиной. Поэтому можно считать, что волны распространяются в тонком поверхностном слое жид-кости. Диаметр Для определения скорости распространения волны удобно рассмотреть движение частиц жидкости на поверхности в сис-теме координат, жестко связанной с движущейся волной. В случае маленьких амплитуд На гребне относительная скорость частиц меньше, чем во впадине, на удвоенную величину ее абсолютной скорости. Это уменьшение скорости частицы при поднятии на гребень объясняется увеличением ее потенциальной энергии. Для гравитационных волн (так называют один из видов по-верхностных волн), в образовании которых основную роль иг-рают силы тяжести, по сравнению с которыми силы поверх-ностного натяжения пренебрежимо малы, это изменение по-тенциальной энергии
где
Изменение кинетической энергии
По закону сохранения энергии
В случае малых амплитуд очертание волны можно считать синусоидальным. Для гармонических колебаний
Учитывая это, из (10.3) и (10.4) следует выражение для скорости поверхностных волн, обусловленных влиянием силы тяжести:
С ростом длины волны Влияние поверхностного натяжения на величину потенци-альной энергии можно учесть следующим образом. Рассмот-рим вертикальное сечение волны, приведенное на рис. 10.1. Волна распространяется в направлении линии АВ по поверх-ности жидкости плотностью
Если в процессе распространения волны точка Р поднима-ется на бесконечно малую высоту
где Работа, совершаемая при подъеме элемента поверхности
где Можно считать, что жидкость, необходимая для напол-нения освободившегося при перемещении элемента поверх-ности пространства, берется с уровня АQВ. Тогда работа, со-вершаемая против силы тяжести, равна
Множитель
где
Если зафиксировать положение волны в какой-то момент времени
В рассматриваемом случае малых амплитуд Следовательно,
Подставляя значение крутизны (10.10) в соотношение (10.7), получим:
Из соотношения (10.11) видно, что поверхностное натяжение как бы увеличивает ускорение силы тяжести на величину Учитывая это, можно видоизменить соотношение (10.5) для скорости волны применительно к общему случаю с уче-том как силы тяжести, так и поверхностного натяжения:
Выражение под знаком корня есть сумма двух слагаемых, изменяющихся в противоположном направлении при изме-нении длины волны. Значение длины волны, соответствующее минимальной скорости, разграничивает область волн, обус-ловленных действием силы тяжести (гравитационных), от об-ласти так называемых капиллярных волн, в образовании кото-рых основную роль играет поверхностное натяжение жидкос-ти. Для чисто капиллярных волн
В общем случае из (10.12) можно получить выражение ко-эффициента поверхностного натяжения, выражая скорость
Соотношение (10.14) используется при определении коэф-фициента поверхностного натяжения жидкости волновым ме-тодом. Поверхностные волны в общем случае (10.12) обладают дисперсией скорости. На реках или водоемах это проявляется в том, что при прохождении какого-либо судна на берегу вна-чале слышны редкие, а потом все более частые затухающие всплески. Это объясняется тем, что длинные волны имеют бóль-шую скорость. Выше мы определяли фазовую скорость по-верхностных волн. Реальное движение происходит с группо-вой скоростью, которая превышает фазовую (10.12) для длин волн меньших длины волны, соответствующей минимальной фазовой скорости, и меньше нее в противоположном случае. В тех случаях, когда
Это единственный вид поверхностных волн, не обладаю-щих дисперсией. Поверхностные волны обладают всеми свойствами, прису-щими всем остальным видам волновых процессов. Так, при одновременном распространении нескольких волн колебания частиц оказываются геометрической суммой колебаний, кото-рые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны накладываются друг на друга, не возмущая одна другую (принцип супер-позиции). Если колебания, обусловленные волнами, возбужденными различными источниками, когерентны, т.е. обладают постоян-ной разностью фаз в каждой точке среды, при их сложении наблюдается явление интерференции. Интерференция прояв-ляется в том, что в одних местах волны усиливают, а в других ослабляют друг друга. В данной работе явление интерференции наблюдается при сложении волн, источниками которых являются отверстия в непроницаемом экране, установленном в воде на пути распро-странения первичных поверхностных волн, возбуждаемых виб-ратором. При этом на экране диаскопа лабораторной установ-ки в местах увеличения амплитуды волновые поверхности имеют меньшую освещенность, а в местах ослабления ампли-туды – бóльшую освещенность. Расчет амплитуды колебаний после прохождения через от-верстия связан со сложными математическими операциями, что затрудняет восприятие происходящих физических явле-ний. В связи с этим ниже дифракция и интерференция волн рассматриваются упрощенно, однако с сохранением основных качественных особенностей рассматриваемых процессов. При прохождении волн через одно отверстие в непроница-емом экране дифракционная картина имеет вид, изображен-ный на рис. 10.2, а, и качественно может быть объяснена с по-мощью принципа Гюйгенса. При квазимонохроматическом ха-рактере колебаний их частота после прохождения через от-верстие остается неизменной, а интенсивность существенно снижается. При размерах отверстия, сопоставимых с длиной волны колебаний, первый волновой фронт (например, макси-мум амплитуды) сформируется на удалениях порядка При прохождении поверхностных волн через два отверс-тия, расстояние между которыми сопоставимо с их размера-ми, наблюдается интерференция волн, которая проявляется в искривлении волновых поверхностей (рис. 10.2, б) на неболь-ших удалениях от экрана. При прохождении поверхностных волн через
|

 траекторий поверхностных частиц жидкос-ти равен разности между впадиной и гребнем. Период
траекторий поверхностных частиц жидкос-ти равен разности между впадиной и гребнем. Период  пол-ного обращения частицы соответствует продвижению волны на полную ее длину
пол-ного обращения частицы соответствует продвижению волны на полную ее длину 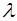 . На гребне волны частица движется в направлении распространения волны, во впадине – в противо-положном направлении.
. На гребне волны частица движется в направлении распространения волны, во впадине – в противо-положном направлении.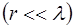 наблюдатель, движущий-ся вместе с волной, видит частицы, проносящиеся по поверх-ности "застывшей" волны в сторону, противоположную дви-жению волны. Во впадине эта относительная скорость части-цы равна
наблюдатель, движущий-ся вместе с волной, видит частицы, проносящиеся по поверх-ности "застывшей" волны в сторону, противоположную дви-жению волны. Во впадине эта относительная скорость части-цы равна  , где
, где  – скорость волны,
– скорость волны,  – абсолютная скорость частицы.
– абсолютная скорость частицы. равно весу
равно весу  , умноженному на высоту:
, умноженному на высоту: , (10.1)
, (10.1) – ускорение силы тяжести;
– ускорение силы тяжести; – масса частицы.
– масса частицы. можно определить из соотношения:
можно определить из соотношения: . (10.2)
. (10.2) , т.е.
, т.е. . (10.3)
. (10.3) (10.4)
(10.4) . (10.5)
. (10.5) и с поверхностным натяже-нием
и с поверхностным натяже-нием  (для воды
(для воды  ,
, 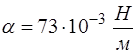 ). Линия АQВ – это уровень спокойной поверхности воды,
). Линия АQВ – это уровень спокойной поверхности воды,  – высота точки Р волновой поверхности над линией АВ.
– высота точки Р волновой поверхности над линией АВ.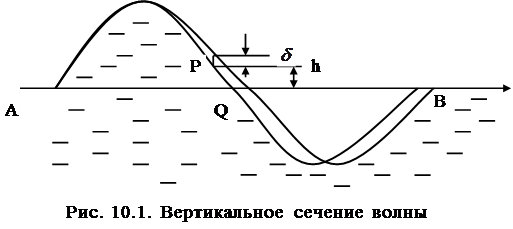
 , то малый элемент по-верхности
, то малый элемент по-верхности  , включающий точку Р, будет двигаться вверх против действия силы, равной
, включающий точку Р, будет двигаться вверх против действия силы, равной
 – модуль радиуса кривизны вертикального сечения вол-ны в точке Р.
– модуль радиуса кривизны вертикального сечения вол-ны в точке Р. , (10.6)
, (10.6) – угол между вертикалью и радиусом кривизны верти-кального сечения волны в точке Р.
– угол между вертикалью и радиусом кривизны верти-кального сечения волны в точке Р. . Вся совершаемая при перемещении элемента поверхности
. Вся совершаемая при перемещении элемента поверхности 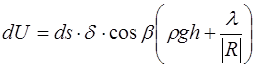 . (10.7)
. (10.7) может быть вычислен из следующих сооб-ражений. Запишем уравнение бегущей волны в виде:
может быть вычислен из следующих сооб-ражений. Запишем уравнение бегущей волны в виде: , (10.8)
, (10.8) – текущее время;
– текущее время; – координата вдоль оси АВ.
– координата вдоль оси АВ. (10.9)
(10.9) вто-рой член в квадратных скобках можно опустить.
вто-рой член в квадратных скобках можно опустить. (10.10)
(10.10) (10.11)
(10.11) .
. . (10.12)
. (10.12)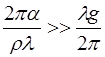 и скорость
и скорость . (10.13)
. (10.13) через частоту колебаний
через частоту колебаний  (частота колебаний вибратора) и длину волны
(частота колебаний вибратора) и длину волны  , то
, то (10.14)
(10.14) , где
, где  – глубина водоема (приливные волны):
– глубина водоема (приливные волны): (10.15)
(10.15) от центра отверстия, а радиусы последующих аналогичных волновых фронтов будут последовательно увеличиваться на величину
от центра отверстия, а радиусы последующих аналогичных волновых фронтов будут последовательно увеличиваться на величину  отверстий интерференционная картина будет иметь вид, приведенный на рис. 10.2, в. Сущность процесса формирования волнового фрон-та в этом случае практически та же, что и при сложении волн в случае двух отверстий.
отверстий интерференционная картина будет иметь вид, приведенный на рис. 10.2, в. Сущность процесса формирования волнового фрон-та в этом случае практически та же, что и при сложении волн в случае двух отверстий.



