Полный факторный эксперимент
1. Для построения математических моделей "Операций" применяют полный факторный эксперимент (ПФЭ). Ортогональность матрицы планирования ПФЭ позволяет получить раздельные оценки для коэффициентов в уравнении регрессии. 2. ПФЭ называется эксперимент, реализующийвсе возможные неповторяющиеся комбинации уровней независимых переменных Х1, Х2, …, Хn, каждая из которых принудительно варьируется на двух уровнях. 3. Математическая модель ищется в виде неполного квадратичного уравнения регрессии взаимосвязи показателя качества "Операции" y от управляемых параметров. Например, для трех факторов это уравнение вида y= b0 + или с учетом линеаризации путем замены переменныхэто y= где xi =
Di - интервал варьирования i -ой переменной. 4. Матрицу планирования ПФЭ и результаты опытов представляют в виде таблицы 1. Например для ПФЭ типа23 , Таблица 4
где x0 – “фиктивная” переменная; xi – кодированные по формуле (2.3) значения переменных; z0 – новые переменные (после линеаризации); y1, у2, …, ym - m параллельных наблюдений показателя качества у для каждого опыта. “+”; ”–” – кодированная запись +1 и –1 соответственно. 5. Так как изменение показателя качества у носит случайный характер, то в каждой точке
6. Перед реализацией плана на объекте необходимо рандомизировать варианты проведения эксперимента, т.е. последовательность реализации опытов матрицы проводить случайно. 7. Проверка воспроизводимости заключается в проверке однородности выборочных дисперсий, т.е. в проварке гипотезы H0: s2{y1} = s2{y2} = … = s2{yN}; при экспериментах соответственно в точках Для этих целей используется критерий Кохрена GP = с числами степеней свободы для числителя n1 =m - 1и знаменателя n2 = N. Если вычисленное значение критерия GP окажется меньше значения Gкр, найденного по статистической таблице для выбранного уровня значимости q, то Н0 принимается. Тогда оценка дисперсии воспроизводимости будет равна
Оценки дисперсий
8. Независимые оценки коэффициентов в уравнении регрессии (2.2) ищутся по формуле
9. Значимость коэффициентов регрессии bi проверяется с помощью t – критерия Стьюдента, который в этом случае преобразуется к виду
где
- дисперсия ошибки определения коэффициентов регрессии. Если вычисленное значение 10. Проверка адекватности полученной модели проводится по F - критерию Фишера: FP = где
d - число значимых коэффициентов уравнения регрессии. Если вычисленное значениеFP критерия меньше Fкр найденного по статистической таблице для соответствующих степеней свобода n1 = N - d и n2 = N(m - 1) при заданном уровне значимости q, то гипотеза об адекватности принимается. Полученная модель признается годной для дальнейших исследований. Проверка адекватности возможна только при n1 > 0, Если n1 = 0, то адекватность проверить нельзя. 11. Порядок выполнения задания. 11.1. Выбрать вид модели (регрессионного уравнения) 11.2. Выбрать матрицу планирования, сформировать таблицу 4. 11.3. Вычислить осредненные значения 11.4. Проверить воспроизводимость по критерию Кохрена. 11.5. Вычислить оценки коэффициентов регрессии. Записать уравнение. 11.6. Проверить значимость коэффициентов bi, по критерию Стьюдента. Сформировать, если нужно новое уравнение регрессии. 11.7. Проверить адекватность полученного уравнения. 11.8. Сделать выводы, оформить задание.
|

 +
+  + b123x1 x2 x3 (2.1)
+ b123x1 x2 x3 (2.1) (2.2)
(2.2) (1£ i £ n) (2.3)
(1£ i £ n) (2.3) - нулевой уровень варьирования i -ой переменной;
- нулевой уровень варьирования i -ой переменной;
 (1 £ i £ N = 2n) надо проводить m параллельных опытов и результаты наблюдений
(1 £ i £ N = 2n) надо проводить m параллельных опытов и результаты наблюдений  ,
, 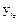 , …,
, …,  (см. последние столбца таблицы 4) усреднить
(см. последние столбца таблицы 4) усреднить =
=  , 1£ i £ N (2.4)
, 1£ i £ N (2.4) ,
,  ,…,
,…,  .
.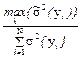 (2.5)
(2.5) {y} =
{y} =  (2.6)
(2.6) (2.7)
(2.7) =
=  , (g = 0, 1, …, n). (2.8)
, (g = 0, 1, …, n). (2.8) =
=  , (q = 0, 1, …, n) (2.9)
, (q = 0, 1, …, n) (2.9) =
=  , (для всех i) (2.10)
, (для всех i) (2.10) , (2.11)
, (2.11) =
=  (2.12)
(2.12)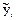 .
.


