Определение. Точки максимума и минимума функции называются точками экстремума.
3. Сыдыкова Д.К. Математика I. Методическое руководство к выполнению заданий для СРС. -Алматы: КазГАСА, 2008. 4. Сыдыкова Д.К. «Курс Математики- I», Модуль I, II для дистанционного обучения. Электронный учебник.-Алматы: КазГАСА, 2012. 5. www.studentlibrary.ru 6. http://sferaznaniy.ru/vysshaya-matematika. Глоссарий
Литература: Основная
2. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах: Учебное пособие для втузов. - М.: Оникс, 2007. Дополнительная 3. Сыдыкова Д.К. Математика I. Методическое руководство к выполнению заданий для СРС. -Алматы: КазГАСА, 2008. 4. Сыдыкова Д.К. «Курс Математики- I», Модуль I, II для дистанционного обучения. Электронный учебник.-Алматы: КазГАСА, 2012. 5. www.studentlibrary.ru 6. http://sferaznaniy.ru/vysshaya-matematika. Определение. Точки максимума и минимума функции называются точками экстремума. Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х1 и точка х1 является точкой экстремума, то производная функции обращается в нуль в этой точке. Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю. Теорема. (Достаточные условия существования экстремума) Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х1, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х1). Если при переходе через точку х1 слева направо производная функции f¢(x) меняет знак с “+” на “-“, то в точке х = х1 функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет минимум. На основе вышесказанного можно выработать единый порядок действий при нахождении наибольшего и наименьшего значения функции на отрезке:
1) Найти критические точки функции. 2) Найти значения функции в критических точках. 3) Найти значения функции на концах отрезка. 4) Выбрать среди полученных значений наибольшее и наименьшее. Исследование функции на экстремум с помощью производных высших порядков.
Пусть в точке х = х1 f¢(x1) = 0 и f¢¢(x1) существует и непрерывна в некоторой окрестности точки х1.
Теорема. Если f¢(x1) = 0, то функция f(x) в точке х = х1 имеет максимум, если f¢¢(x1)<0 и минимум, если f¢¢(x1)>0. Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой. Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла). Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная пересекает кривую. Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f¢¢(a) = 0 или f¢¢(a) не существует и при переходе через точку х = а f¢¢(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба. При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой. Определение. Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю. Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой. Вообще говоря, кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как показано на приведенном ниже графике функции
Рассмотрим подробнее методы нахождения асимптот кривых. Вертикальные асимптоты. Из определения асимптоты следует, что если Наклонные асимптоты. Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b.
Отметим, что горизонтальные асимптоты являются частным случаем наклонных асимптот при k =0. Схема исследования функций 1) Область существования функции. Это понятие включает в себя и область значений и область определения функции. 2) Точки разрыва. (Если они имеются). 3) Интервалы возрастания и убывания. 4) Точки максимума и минимума. 5) Максимальное и минимальное значение функции на ее области определения. 6) Области выпуклости и вогнутости. 7) Точки перегиба. (Если они имеются). 8) Асимптоты. (Если они имеются). 9) Построение графика.
|

 . Ее наклонная асимптота у = х.
. Ее наклонная асимптота у = х.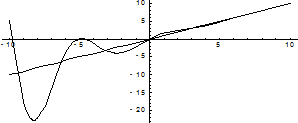
 или
или  или
или  , то прямая х = а – асимптота кривой y = f(x).
, то прямая х = а – асимптота кривой y = f(x).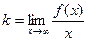 ,
, 



