ЗАТУХАЮЩИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
В реальных условиях, кроме возвращающей силы в колебательной системе обязательно будет действовать и сила сопротивления. Будем считать, что скорости движения при колебаниях будут небольшими, тогда сила сопротивления прямо пропорциональна скорости:
где r –коэффициент сопротивления. Учитывая только силу сопротивления (13) и силу упругости (1) согласно II закону Ньютона для уравнения движения получим:
Разделив правую и левую часть (15) на m и обозначив k/m =
Это однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение: к2 + 2b·к + w
Из (17) видно, что движение будет колебательным, только если b2 < w
Теперь решением уравнения (16) будет функция:
s= е-βt(С1cosωt + C2sinωt).
Заменяя С1 и С2 через другие постоянные А0 и φ0 такие, что С1 = А0cosφ0, а С2 = А0sinφ0 окончательно получим:
s = А0е−βtcos(ωt + φ○) (18).
А = А0 е−βt, (19)
(рис.5, пунктирная линия). Круговая частота этого колебания w = Для описания быстроты затухания колебаний используют три взаимосвязанные величины: коэффициент затухания – β, декремент затухания – δ и логарифмический декремент затухания – λ. Коэффициент затухания b =
и логарифмический декремент затухания
l = ℓ n d = ℓnеβТ = βТ. (21)
|

 , (13)
, (13) , (14)
, (14) . (15)
. (15) , а r/m = 2β, получим:
, а r/m = 2β, получим: или
или  . (16).
. (16). = 0 имеет корни
= 0 имеет корни  . (17)
. (17) , где
, где  .
.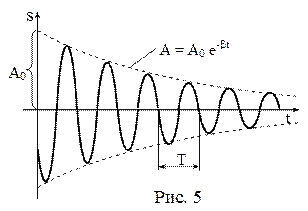 Это уравнение свободных затухающих колебаний, график которых представлен на рис.5. Как видно амплитуда свободных затухающих колебаний убывает по экспоненциальному закону:
Это уравнение свободных затухающих колебаний, график которых представлен на рис.5. Как видно амплитуда свободных затухающих колебаний убывает по экспоненциальному закону: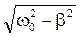 , а период Т = 2π /
, а период Т = 2π /  . Как видно, ни частота, ни период затухающих колебаний не равны соответствующим параметрам собственных колебаний системы.
. Как видно, ни частота, ни период затухающих колебаний не равны соответствующим параметрам собственных колебаний системы. , [b] = 1/с. Декремент затухания –
, [b] = 1/с. Декремент затухания – (20)
(20)


