Колебания, которые совершаются под воздействием переменной силы, называются вынужденными.
Рассмотрим колебания под воздействием вынуждающей силы, изменяющейся по гармоническому закону:
F = F○соsω в t. (22)
С учетом квазиупругой силы (1) и силы сопротивления (13) дифференциальное уравнение вынужденных колебаний запишется:
Разделив правую и левую часть на m, и обозначив:
Решением этого уравнения будет функция:
s = Acos(ω в t + φ0). (25)
Это уравнение установившихся вынужденных колебаний. Здесь:
Как видно из (25), колебания, происходящие под воздействием гармонической вынуждающей силы спустя некоторое время, тоже становятся гармоническими (рис. 6). Их частота равна частоте вынуждающей силы ω в. Из выражения (26) для амплитуды видно, что ее значение зависит от соотношения частоты вынуждающей силы ωв и собственной частоты колебательной системы ωо. Очевидно, если подкоренное выражение
Амплитуда при этом достигает значения:
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте колебательной сис-темы получило название резонанса, а соответствующая частота вынуждающей силы – резонансной частотой колебаний. Приведенные на рис.7 графики, которые называют резонансными кривыми, отличаются значением коэффициента затухания, действующего в колебательной системе. С уменьшением значения β, резонансные кривые становятся все острее, а величина Арез все больше. Теоретически при β → 0 частота ωрез→ ω0, а амплитуда А → ∞.
Резонанс может иметь как полезные, так и вредные последствия. В одних случаях он может вызвать разрушение, и это приходится учитывать при конструировании мостов, самолетов, высотных домов. В других случаях, наоборот, стремятся создать условия для резонанса, например, при изготовлении музыкальных инструментов, в радиотехнике и т.д. Автоколебания (качели, часы, электрический колебательный контур) – незатухающие колебания, поддерживаемые внешним источником энергии. Причем поступление энергии регулируется самой колебательной системой. Параметрические колебания – это колебания, возбуждаемые путем периодического изменения параметров колебательной системы. Пример: шарик на нити, длина которой периодически меняется.
5. СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ ОДНОГО НАПРАВЛЕНИЯ
Возможны случаи, когда тело одновременно участвует в нескольких колебаниях. Например, барабанная перепонка уха одновременно воспринимает колебания от нескольких источников звука – голоса, шум, музыку и т.д. Встает задача получить уравнение результирующего колебания.
Воспользуемся этой геометрической моделью, чтобы найти уравнение результирующего движения, в простейшем случае – сложении двух гармонических колебаний одного направления и с одинаковыми частотами ω:
Построим векторные диаграммы этих колебаний – вектора А1 и А2 (рис.10). Из рисунка видно, что проекция результирующего вектора А на ось Х: х = х 1 + х 2 = Аcos(wt + j0). (31)
Т.к. вектора А1 и А2 вращаются с одинаковыми скоростями ω, то и А будет вращаться с той же скоростью ω, а разность фаз колебаний в процессе движения меняться не будет – φ2 – φ1 = (wt + j0,2) - (wt + j0,1) = j0,2 - j0,1 = const.
Применяя теорему косинусов, из треугольника ОСВ найдем результирующую амплитуду А: А2 = А12 + А22 – 2А1А2 cos β. Но β = π – (φ2 – φ1) = π – (φ02 – φ01), тогда:
А2 = А12 + А22 + 2А1А2 cos(φ02 – φ01). (32)
Для начальной фазы результирующего колебания φ0 из ∆ОВD получим: tg φ0 =
Как видно из выражения (32) для А возможны три случая:
а) φ02 – φ01 = 0; А2 = А12 + А22 + 2А1А2 = (А1 + А2)2; А = А1 + А2.
б) φ02 – φ01 = π; А2 = А12 + А22 - 2А1А2 = (А1 - А2)2; А = А1 - А2.
в) φ02 – φ01 – любое от 0 до π, в этом случае А1 - А2 < А < А1 + А2.
|

 . (23)
. (23) ,
,  ,
,  , после перегруппировки слагаемых, получим неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами:
, после перегруппировки слагаемых, получим неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами: . (24)
. (24)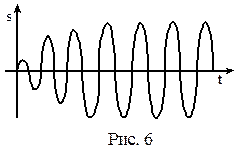
 , (26)
, (26) . (27)
. (27) будет минимально, то амплитуда вынужденных колебаний достигнет своего максимального значения. Исследование на экстремум дает: -2(ω02 – ωв2) ·2ωв + 8β2ωв = 0, ωв2 - ω02 + 2β2 = 0, что будет иметь место, если
будет минимально, то амплитуда вынужденных колебаний достигнет своего максимального значения. Исследование на экстремум дает: -2(ω02 – ωв2) ·2ωв + 8β2ωв = 0, ωв2 - ω02 + 2β2 = 0, что будет иметь место, если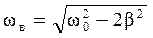 . (28)
. (28) Арез =
Арез =  . (29)
. (29) Как показывает сопоставление (22) и (25), вынужденные колебания тела отстают по фазе от колебаний вынуждающей силы на φ0. График зависимости φ 0 от ωв при различных значениях β приведен на рис.8.
Как показывает сопоставление (22) и (25), вынужденные колебания тела отстают по фазе от колебаний вынуждающей силы на φ0. График зависимости φ 0 от ωв при различных значениях β приведен на рис.8.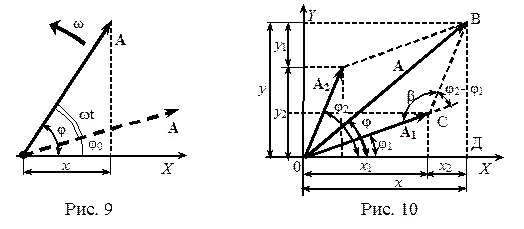
 (30)
(30)
 . (33)
. (33)


