Колебательные движения. Основные характеристики колебательного процесса.
ФЭЛ-2
Изучение затухающих колебаний
Тула, 2009 г
Изучение затухающих колебаний Цель работы: с помощью встроенного генератора импульсов и электронного осциллографа получить затухающие электромагнитные колебания; определить период электромагнитных колебаний, логарифмический декремент затухания, коэффициент затухания и другие параметры колебательного контура. Теоретическое описание. Колебательные движения. Основные характеристики колебательного процесса. Колебаниями, или колебательными движениями, называются движения, обладающие той или иной степенью повторяемости во времени. По своей физической природе колебания весьма разнообразны. К ним относятся механические колебания (качание маятника, колебания струны, стержней и т.д.), электромагнитные колебания и др. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через одинаковый промежуток времени. Периодом колебаний T называется тот наименьший промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебательное движение точки. За это время совершается одно полное колебание. Частотой периодических колебаний ν; называется число полных колебаний, совершаемых за единицу времени:
Простейшим типом периодических колебаний являются гармонические (синусоидальные) колебания. В этом случае смещение колеблющейся точки происходит по гармоническому закону:
Величина х0 (наибольшее значение отклонения точки от положения равновесия) называется амплитудой колебаний, Дифференциальное уравнение, которому удовлетворяет величина х, имеет следующий вид:
Если на колеблющееся тело действует сила трения, то энергия системы, а вместе с ней и амплитуда колебаний убывают (энергия расходуется на работу против сил трения и превращается в тепло). Происходит постепенное затухание колебаний (рис. 1). Затухающие колебания не являются гармоническими. При рассмотрении негармонических колебаний, строго говоря, уже нельзя употреблять термин "амплитуда", он имеет определенный смысл только для гармонических колебаний. Однако этот термин применяют и к негармоническим колебаниям, понимая под амплитудой наибольшее значение, которого достигает смещение в течение одного периода колебаний. Закон убывания амплитуды колебаний зависит от характера сил трения, действующих на колеблющееся тело.
Наиболее простым и вместе с тем распространенным является случай, когда сила трения f пропорциональна скорости колеблющегося тела:
В этом случае уравнение движения имеет следующий вид:
где т - степень "сопротивления" системы внешним воздействиям, ее инертность (масса - в механике, индуктивность - в электромагнитных явлениях); b - степень замедления движения из-за необратимой диссипации энергии (коэффициент трения, активное сопротивление); k - степень стремления к положению равновесия (коэффициент упругости в механике, величина обратная электроемкости в электричестве); F - внешняя (вынуждающая) сила. Если F постоянна или отсутствует, то колебания называются собственными или свободными. Основные параметры колебаний определяются свойствами самой колебательной системы, за исключением амплитуды, которая задается начальной энергией. Решение уравнения (1.5) имеет вид:
где
x0, φ0 – константы, зависящие от начальных условий колебательного процесса. Амплитуда затухающих колебаний убывает с течением времени по экспоненциальному закону:
Если в некоторый момент времени t1 амплитуда колебаний имеет значение,
Таким образом, отношение значений двух последовательных амплитуд колебаний:
есть величина постоянная, называемая декрементом затухания. Натуральный логарифм этого отношения:
называется логарифмическим декрементом затухания. Логарифмический декремент затухания - величина, обратная числу колебаний N, по истечении которых амплитуда уменьшается в е раз: Промежуток времени τ, необходимый для этого, называется временем релаксации:
В зависимости от величины τ колебания в контуре получается слабо или сильно затухающими. Чем меньше трение и чем больше т, тем меньше затухание, то есть тем ближе кривая (1.6) приближается к синусоиде (1.2). При значительном возрастании трения декремент затухания так же, как и период:
увеличивается. При В настоящей работе определение параметров затухающего колебательного процесса проводится для электрического колебательного контура, состоящего из катушки индуктивности L и емкости С.
|

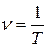 (1.1)
(1.1)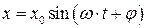 (1.2)
(1.2)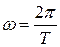 - круговая (или циклическая) частота колебаний,
- круговая (или циклическая) частота колебаний, 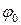 - начальная фаза наблюдений.
- начальная фаза наблюдений.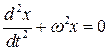 (1.3)
(1.3)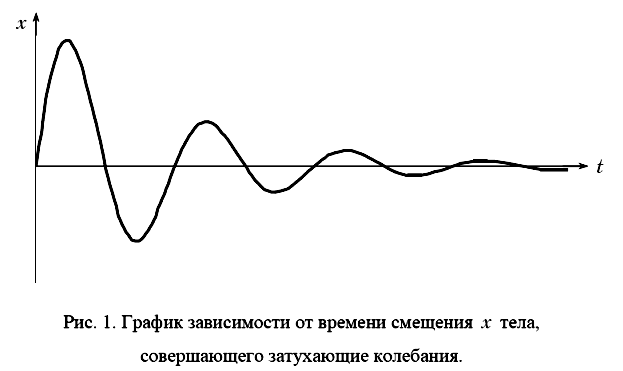
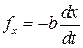 (1.4)
(1.4)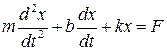 (1.5)
(1.5)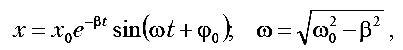 (1.6)
(1.6)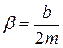 - коэффициент затухания;
- коэффициент затухания;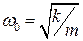 - циклическая частота свободных колебаний системы в отсутствии трения;
- циклическая частота свободных колебаний системы в отсутствии трения;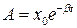 (1.7)
(1.7)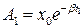 , то через период T ее значение будет
, то через период T ее значение будет 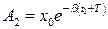 . Отношение обоих значений равно:
. Отношение обоих значений равно: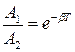 (1.8)
(1.8)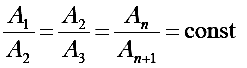 (1.9)
(1.9)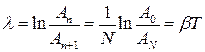 (1.20)
(1.20)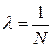 (e – основание натуральных логарифмов).
(e – основание натуральных логарифмов).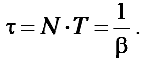 (1.21)
(1.21)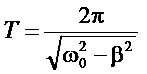 (1.22)
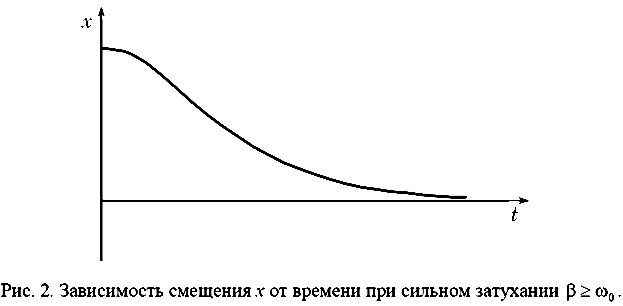
(1.22)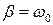 выражение (1.22) обращается в бесконечность и движение из колебательного превращается в апериодическое (рис. 2).
выражение (1.22) обращается в бесконечность и движение из колебательного превращается в апериодическое (рис. 2).