Колебательный контур. Затухающие электрические колебания.
В данной работе колебательный процесс изучается на примере электрических затухающих колебаний. В цепи, содержащей катушку индуктивности L и конденсатор емкости С могут возникать электрические колебания, при которых электрические величины (заряды, токи, электрические и магнитные поля) изменяются периодически. Переменное электромагнитное поле распространяется в пространстве со скоростью, равной скорости света (с=3∙108м/с). Поэтому, если линейные размеры Рассмотрим идеализированный контур, сопротивление которого пренебрежимо мало (R=0). Если зарядить конденсатор от батареи до напряжения В начальный момент, когда конденсатор полностью заряжен, в нем накоплена электрическая энергия:
где Во время разряжения конденсатора электрическая энергия превращается в энергию магнитного поля катушки и когда конденсатор полностью разряжен вся электрическая энергия переходит в магнитную:
где При перезарядке конденсатора энергия магнитного поля снова превращается в энергию электрического поля. В контуре возникают незатухающие электромагнитные колебания, т.е. периодически изменялись (колебались) бы заряд q на обкладках конденсатора, напряжение U на конденсаторе и сила тока I, текущего через катушку индуктивности. По второму правилу Кирхгофа для контура при
где
где
Подставим последнее выражение в (2.3), получим дифференциальное уравнение незатухающих гармонических колебаний:
Решением этого уравнения является:
где
а период собственных незатухающих колебаний:
Однако, в реальности проводники контура всегда обладают электрическим сопротивлением, поэтому часть энергии в процессе колебаний расходуется на нагрев проводников. Вследствие этого амплитуда электромагнитных колебаний в контуре постепенно уменьшается, и в нем происходят затухающие колебания. Рассмотрим реальный колебательный контур, содержащий катушку индуктивности L, конденсатор емкостью С и сопротивление R (рис.1,в). По второму правилу Кирхгофа для такого контура:
где Используя соотношения (2.4), (2.5) и (2.6), уравнение (2.8) примет вид:
Дифференциальное уравнение (2.9) описывает затухающие колебания. Его решением является:
где Изменение напряжения на конденсаторе от времени графически представлено на рис.2 Коэффициент затухания
Циклическая частота затухающих колебаний
при этом
 и и  (2.13) (2.13)
Если (2.8) записать в виде На практике вместо коэффициента затухания β обыкновенно употребляется другая мера затухания, а именно логарифмический декремент затухания (1.20):
называется критическим. Электрический контур часто характеризуют добротностью Q:
где W(t), W(t+T) – энергия контура в моменты времени t и t+T. Так как энергия W(t) пропорциональна квадрату амплитуды колебаний соответствующей величины, например U, то:
Учитывая периодичность функции косинуса:
При малых значениях логарифмического декремента затухания величина 1-e-2λ≈2λ и добротность контура:
|

 контура не слишком велики (
контура не слишком велики ( , где
, где  - частота колебаний в контуре), то можно считать, что в каждый момент времени t сила тока I во всех частях контура одинакова. Такой переменный ток называется квазистационарным. Это позволяет нам использовать тот факт, что мгновенные значения квазистационарных токов подчиняются закону Ома.
- частота колебаний в контуре), то можно считать, что в каждый момент времени t сила тока I во всех частях контура одинакова. Такой переменный ток называется квазистационарным. Это позволяет нам использовать тот факт, что мгновенные значения квазистационарных токов подчиняются закону Ома. (рис.1,а), а затем замкнуть переключатель
(рис.1,а), а затем замкнуть переключатель  , то конденсатор начнет разряжаться через катушку; в ней появляется ток
, то конденсатор начнет разряжаться через катушку; в ней появляется ток  , создающий магнитное поле (рис.1,б), и в контуре возникнут электромагнитные колебания. Изменение магнитного поля тока приводит к возникновению в цепи электродвижущей силы самоиндукции Еi, замедляющий быстроту разряда. При уменьшении тока возникает электродвижущая сила, направленная в ту же сторону, что и вызвавший ее появление ток. Это приводит к тому, что после разряда конденсатора ток не прекращается сразу, а в течение некоторого времени продолжает течь в том же направлении и перезаряжает обкладки конденсатора. Затем процесс разряда начинается снова, но протекает теперь в обратном направлении. В результате вторичного перезарядке конденсатора система возвращается в исходное состояние, после чего происходит повторение тех же процессов. Время в течение, которого конденсатор заряжается и разряжается, называется периодом собственных колебаний.
, создающий магнитное поле (рис.1,б), и в контуре возникнут электромагнитные колебания. Изменение магнитного поля тока приводит к возникновению в цепи электродвижущей силы самоиндукции Еi, замедляющий быстроту разряда. При уменьшении тока возникает электродвижущая сила, направленная в ту же сторону, что и вызвавший ее появление ток. Это приводит к тому, что после разряда конденсатора ток не прекращается сразу, а в течение некоторого времени продолжает течь в том же направлении и перезаряжает обкладки конденсатора. Затем процесс разряда начинается снова, но протекает теперь в обратном направлении. В результате вторичного перезарядке конденсатора система возвращается в исходное состояние, после чего происходит повторение тех же процессов. Время в течение, которого конденсатор заряжается и разряжается, называется периодом собственных колебаний.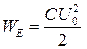 , (2.1)
, (2.1) - максимальное напряжение на конденсаторе.
- максимальное напряжение на конденсаторе. , (2.2)
, (2.2) - наибольшая величина тока в контуре.
- наибольшая величина тока в контуре. :
: , (2.3)
, (2.3) - напряжение на конденсаторе;
- напряжение на конденсаторе;  - ЭДС самоиндукции, возникающая в катушке при протекании в ней переменного тока.
- ЭДС самоиндукции, возникающая в катушке при протекании в ней переменного тока. , (2.4)
, (2.4)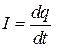 , (2.5)
, (2.5) так как
так как  , то из (2.4) и (2.5) получаем:
, то из (2.4) и (2.5) получаем: ,
,  . (2.6)
. (2.6) . (2.7)
. (2.7) ,
, - амплитудное значение напряжения, которое не зависит от времени;
- амплитудное значение напряжения, которое не зависит от времени;  - собственная частота контура, равная:
- собственная частота контура, равная: ,
, .
. (2.8)
(2.8) - напряжение на сопротивлении.
- напряжение на сопротивлении. (2.9)
(2.9) , (2.10)
, (2.10) - коэффициент затухания,
- коэффициент затухания, 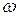 - частота затухающих колебаний.
- частота затухающих колебаний. , (2.11)
, (2.11)
 (2.12)
(2.12)
 и продифференцировать по времени, то получим уравнение того же типа, что и уравнение (2.9)
и продифференцировать по времени, то получим уравнение того же типа, что и уравнение (2.9)  из чего следует, что ток в контуре также совершает затухающие колебания, для которых значение β,
из чего следует, что ток в контуре также совершает затухающие колебания, для которых значение β, 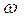 и Т определяется по формулам (2.11), (2.12) и (2.13).
и Т определяется по формулам (2.11), (2.12) и (2.13). (2.14)
(2.14)
 Из формул (2.12) и (2.13) следует, что в контуре возможны затухающие колебания лишь в том случае, если
Из формул (2.12) и (2.13) следует, что в контуре возможны затухающие колебания лишь в том случае, если  →
→  (частота и период - действительные величины). Если
(частота и период - действительные величины). Если  , то частота и период - мнимые, колебаний нет, и происходит апериодический разряд конденсатора (рис.3). Сопротивление:
, то частота и период - мнимые, колебаний нет, и происходит апериодический разряд конденсатора (рис.3). Сопротивление: (2.15)
(2.15) (2.16)
(2.16)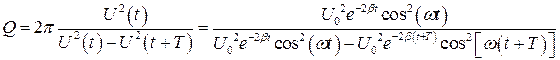 (2.17)
(2.17) и производя сокращения в формуле (2.17), получим:
и производя сокращения в формуле (2.17), получим: (2.18)
(2.18) (2.19)
(2.19)


