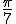Еще одним известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.
Типичный представитель данного класса фракталов "Плазма" (см. рис. 4). Для ее построения возьмем прямоугольник и для каждого его угла определим цвет. Далее находим центральную точку прямоугольника и раскрашиваем ее в цвет равный среднему арифметическому цветов по углам прямоугольника плюс некоторое случайное число. Чем больше случайное число - тем более "рваным" будет рисунок. Если мы теперь скажем, что цвет точки это высота над уровнем моря - получим вместо плазмы - горный массив. Именно на этом принципе моделируются горы в большинстве программ. С помощью алгоритма, похожего на плазму строится карта высот, к ней применяются различные фильтры, накладываем текстуру и, пожалуйста, фотореалистичные горы готовы.
Рис. 4. "Плазма"
| № варианта
| Изображение
| Описание
|
| Аналитические фракталы
|
|
| 
| Множество Мандельброта  x Î(-2,2; 1),
y Î(-1,2; 1,2).
Условие остановки цикла
x Î(-2,2; 1),
y Î(-1,2; 1,2).
Условие остановки цикла 
|
|
| 
| 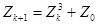
|
|
| 
| 
|
|
| 
| 
|
|
| 
| Множество Жулиа
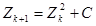 ,
С=0,36+ i ×0,36,
x Î(-1; 1), y Î(-1,2; 1,2).
Условие завершения цикла ,
С=0,36+ i ×0,36,
x Î(-1; 1), y Î(-1,2; 1,2).
Условие завершения цикла  . .
|
|
| 
| Множество Жулиа С=0,32+ i ×0,043
|
|
| 
| Множество Жулиа
С =-0,39054- i ×0,58679
|
|
| 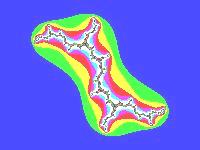
| Множество Жулиа
С= i
|
|
| 
| Множество Жулиа 
|
|
| 
| Множество Жулиа 
|
|
| 
| Крест Ньютона  .
x Î(-1; 1), y Î(-1; 1). Условие остановки цикла .
x Î(-1; 1), y Î(-1; 1). Условие остановки цикла 
|
| L-системы
|
|
| 
| Кривая Коха Аксиома: F Правило: F → F-F++F-F Угол: 
|
|
| 
| Снежинка Коха Аксиома: F++F++F Правило: F → F-F++F-F Угол: 
|
|
| 
| Аксиома: F+F+F Правило: F → F-F+F Угол: 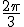
|
|
| 
| Аксиома: F+F+F+F Правило: F → FF+F++F+F Угол:  Ледяные фракталы Ледяные фракталы
|
|
| 
| Кривая дракона Аксиома: FX Правила: X → X+YF+ Y → -FX-Y Угол: 
|
|
| 
| Кривая Госпера Аксиома: XF Правила: X → X+YF++YF-FX--FXFX-YF+ Y → -FX+YFYF++YF+FX--FX-Y Угол: 
|
|
| 
| Кривая Серпинского Аксиома: F+XF+F+XF Правило: X → XF-F+F-XF+F+XF-F+F-X Угол: 
|
|
| 
| Кривая Гильберта Аксиома: X Правила: X → -YF+XFX+FY- Y → +XF-YFY-FX+ Угол: 
|
|
| 
| Аксиома: F+F+F+F Правило: F → FF+F+F+F+FF Угол: 
|
|
| 
| Аксиома: F+F+F+F Правило: F → F+F-F-FF+F+F-F Угол:  Обобщения кривой Коха Обобщения кривой Коха
|
|
| 
| Аксиома: F+F+F+F Правило: F → F+F-F-FFF+F+F-F Угол:  Обобщения кривой Коха Обобщения кривой Коха
|
|
| 
| Аксиома: F+F+F+F Правило: F → F-FF+FF+F+F-F-FF+F+F-F-FF-FF+F Угол:  Обобщения кривой Коха Обобщения кривой Коха
|
|
| 
| Аксиома: F Правило: F → F-F+F+F-F Угол: 
|
|
| 
| Аксиома: YF Правила: X → YF+XF+Y Y → XF-YF-X Угол: 
|
|
| 
| Аксиома: F+F+F+F Правило: F → F+F-F+F+F Угол: 
|
|
| 
| Аксиома: F+F+F+F Правило: F → FF+F+F+F+F+F-F Угол: 
|
|
| 
| Куст Аксиома: Y Правила: X → X[-FFF][+FFF]FX Y → YFX[+Y][-Y] Угол: 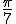
|
|
| 
| Куст Аксиома: F Правило: F → FF+[+F-F-F]-[-F+F+F] Угол: 
|
|
| 
| Куст Аксиома: F Правило: F → F[+FF][-FF]F[-F][+F]F Угол: 
|
|
| 
| Куст Аксиома: X Правила: F → FF X → F[+X]F[-X]+X Угол: 
|
|
| 
| Куст Аксиома: F-F-F-F Правило: F → F-F+F+F-F Угол: 
|
|
| 
| Сорняк Аксиома: F Правило: F → F[+F]F[-F]F Угол: 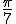
|
|
| 
| Аксиома: F Правила: F → FXF X → [-F+F+F]+F-F-F+ Угол: 
|
|
| 
| Треугольник Серпинского Аксиома: FXF--FF--FF Правила: F → FF X → --FXF++FXF++FXF-- Угол: 
|
|
| 
| Ковёр Серпинского Аксиома: F Правило: F → FFF[+FFF+FFF+FFF] Угол: 
|
|
| 
| Мозаика Аксиома: F-F-F-F Правила: F → F-b+FF-F-FF-Fb-FF+b-FF+F+FF+Fb+FFF b → bbbbbb Угол:  Здесь b означает переместиться вперёд на один шаг, не прорисовывая след. Здесь b означает переместиться вперёд на один шаг, не прорисовывая след.
|
|
| 
| Кривая Леви Аксиома: F++F++F++F Правило: F → -F++F- Угол: 
|
|
| 
| Аксиома: F++F++F++F++F Правило: F → F++F++F+++++F-F++F Угол: 
|
|
| 
| Аксиома: F Правило: F → F+F-F Угол: 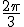
|
|
| 
| Ковёр Серпинского Аксиома: F Правила: F → F+F-F-F-b+F+F+F-F b → bbb Угол:  Здесь b означает переместиться вперёд на один шаг, не прорисовывая след. Здесь b означает переместиться вперёд на один шаг, не прорисовывая след.
|
|
| 
| Аксиома: F-F-F-F-F Правило: F → F-F++F+F-F-F Угол: 
|
|
| 
| Аксиома: X Правила: F → X → -F++F-X-F--F+Y---F--F+Y+F++F-X+++F++F-X-F++F-X+++F--F+Y-- Y → +F++F-X-F--F+Y+F--F+Y---F--F+Y---F++F-X+++F++F-X+++F--F+Y Угол: 
|
|
| 
| Аксиома: FX Правила: F → X → FX-FY-FX+FY+FX+FY+FX+FY+FX-FY-FX-FY-FX-FY-FX+FY+FX Y → FY Угол: 
|
|
| 
| Аксиома: XYXYXYX+XYXYXYX+XYXYXYX+XYXYXYX Правила: F → X → FX+FX+FXFY-FY- Y → +FX+FXFY-FY-FY Угол: 
|
|
| 
| Аксиома: F--F--F--F--F--F Правило: F → -F[--F--F]++F--F+ Угол: 
|
|
| 
| Аксиома: F+F+F Правило: F → F+FF-F Угол: 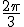
|
|
| 
| Аксиома: X Правила: F → X → FY+FYFY-FY Y → FX-FXFX+FX Угол: 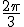
|
|
| 
| Аксиома: X Правила: F → X → FX+FX+FXFYFX+FXFY-FY-FY- Y → +FX+FX+FXFY-FYFXFY-FY-FY Угол: 
|
|
| 
| Аксиома: X-X-X-X-X Правила: F → X → FX-FX-FX+FY+FY+FX-FX Y → FY+FY-FX-FX-FY+FY+FY Угол: 
|
|
| 
| Аксиома: F-F-F-F-F Правило: F → F-F-F++F+F-F Угол: 
|
|
| 
| Аксиома: L--F--L--F Правила: L → +R-F-R+ R → -L+F+L- Угол: 
|
|
| 
| Аксиома: X Правила: X → F-F-F+F+FX++F-F-F+F+FX--F-F-F+F+FX F → Угол: 
|
|
| 
| Аксиома: F++++F Правило: F → F+F+F++++F+F+F Угол: 
|
|
| 
| Аксиома: F+F+F+F++F-F-F-F Правило: F → F+F++F+FF Угол: 
|
|
| 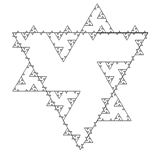
| Аксиома: F++F++F+++F--F--F Правило: F → FF++F++F++FFF Угол: 
|
| Стохастические фракталы
|
|
| 
| Плазма
|



 x Î(-2,2; 1),
y Î(-1,2; 1,2).
Условие остановки цикла
x Î(-2,2; 1),
y Î(-1,2; 1,2).
Условие остановки цикла 

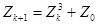





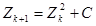 ,
С=0,36+ i ×0,36,
x Î(-1; 1), y Î(-1,2; 1,2).
Условие завершения цикла
,
С=0,36+ i ×0,36,
x Î(-1; 1), y Î(-1,2; 1,2).
Условие завершения цикла 







 .
x Î(-1; 1), y Î(-1; 1). Условие остановки цикла
.
x Î(-1; 1), y Î(-1; 1). Условие остановки цикла 




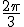

 Ледяные фракталы
Ледяные фракталы