II) Возвратные уравнения и к ним сводящиеся.
Уравнение называется возвратным, если в нем коэффициенты равноудаленные от концов совпадают, т.е.
Возвратные уравнения четной степени.
т.к.
Введем замену. Пусть
Вернемся к замене.
Ответ:
Возвратные уравнения нечетной степени. Любое возвратное уравнение нечетной степени сводится к квадратному уравнению четной степени, т.к у любого возвратного ур–ия нечетной степени один из корней всегда равен –1
Очевидно
т.к уравнения на
Введем замену. Пусть
корней нет Ответ:
III) Уравнения вида
IV) Замена переменных по явным признакам.
V) В следующих уравнениях используется “идея однородности”. Пример №1
Введем замену. Пусть
1) если
2) Разделим обе части уравнения на
Решим последнее уравнение, как квадратное относительно
Вернемся к замене.
Ответ:
Пример №2.
Пусть Найдем Составим систему:
Решая систему подстановкой, получим
корней нет Ответ:
|
, 
, 
- не является корнем уравнения, то разделим обе части уравнения на 
.
, 
, получим
; 
или 
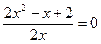
корней нет
- корень уравнения.
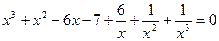
, получим
или 
или 
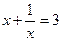
, где 
решаются как возвратные.
, 
, тогда
, тогда 
, тогда
решений нет
, получим
, получим
; 
; 
или 
корней нет
, 
, тогда 
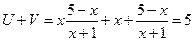
или 
; 
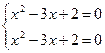
