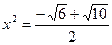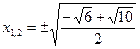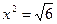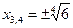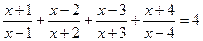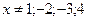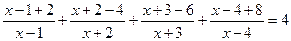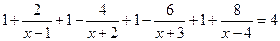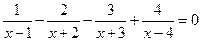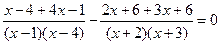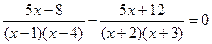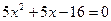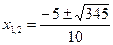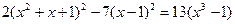
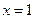 - не является корнем уравнения
- не является корнем уравнения
Разделим обе части уравнения на 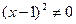 , получим
, получим

Введем замену.
Пусть 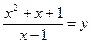 , тогда
, тогда
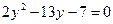
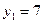 ;
; 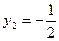
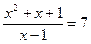 или
или 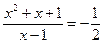
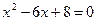
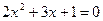
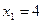 ;
; 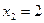
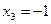 ;
; 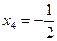
Ответ: 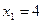 ;
; 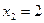 ;
; 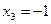 ;
; 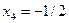
VI) Уравнения вида 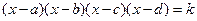 , где
, где 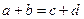 эффективно решать перемножением
эффективно решать перемножением 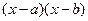 и
и 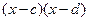 , а затем делать замену.
, а затем делать замену.
VII) В уравнениях вида 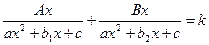 и в уравнениях к ним сводящимся, в знаменателях обоих дробей необходимо вынести х за скобки и сделать замену.
и в уравнениях к ним сводящимся, в знаменателях обоих дробей необходимо вынести х за скобки и сделать замену.
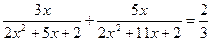 (1)
(1) 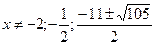
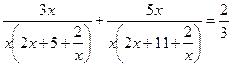 (2)
(2)
При переходе 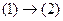 область определения уравнения сузилась на
область определения уравнения сузилась на 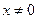 . Проверим, является ли
. Проверим, является ли  корнем уравнения. Не является.
корнем уравнения. Не является.
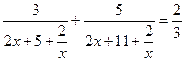
Введем замену.
Пусть 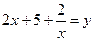 ,
, 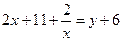 , тогда
, тогда
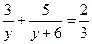
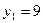 ;
; 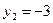
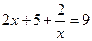 или
или 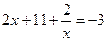
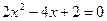
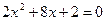
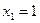

Ответ: 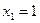 ;
; 
VIII) В уравнениях вида 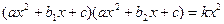 обе части уравнения делятся на
обе части уравнения делятся на 
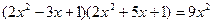
 - не является корнем уравнения. Разделим на
- не является корнем уравнения. Разделим на  , получим
, получим
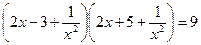
Введем замену.
Пусть 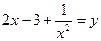 ;
; 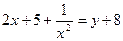 , тогда
, тогда
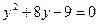
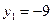 ;
; 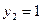
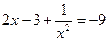 или
или 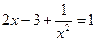
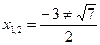
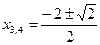
Ответ: 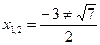 ;
; 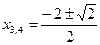
IX) Выделение полного квадрата.
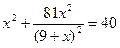
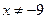
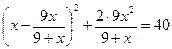
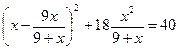
Введем замену.
Пусть 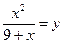 , тогда
, тогда
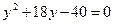
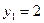 ;
; 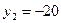
Вернемся к замене.
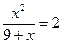 или
или 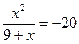
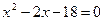
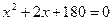
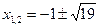 корней нет
корней нет
Ответ: 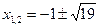
X) Решение уравнений с помощью формулы 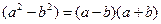
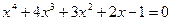
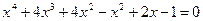
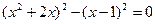
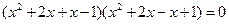
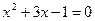 или
или 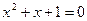
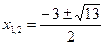 корней нет
корней нет
XI) Уравнения вида 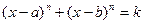 и к ним сводящиеся решаются при помощи замены
и к ним сводящиеся решаются при помощи замены 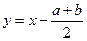
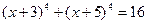
Введем замену.
Пусть 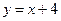 , тогда
, тогда
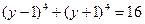
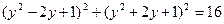
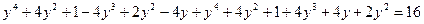
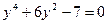
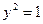 или
или 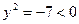 корней нет
корней нет
 ;
; 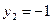
Вернемся к замене.
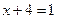 или
или 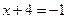
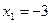
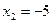
Ответ: 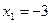 ;
; 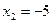
XII) Решение уравнений относительно коэффициентов.
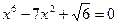
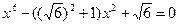
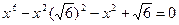
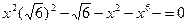
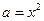
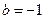
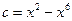
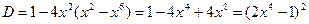
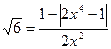 или
или 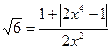
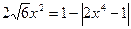
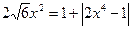

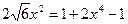
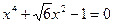
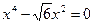
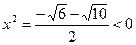 ;
; 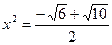
 - посторонний корень
- посторонний корень
корней нет 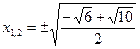
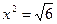
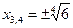
Ответ: 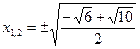 ;
; 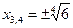
XIII) Метод разложения на простейшие дроби.
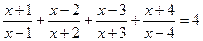
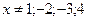
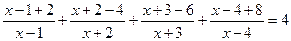
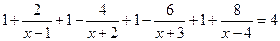
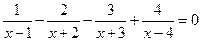
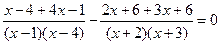
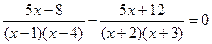
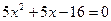
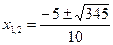
Ответ: 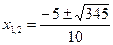

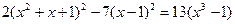
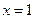 - не является корнем уравнения
- не является корнем уравнения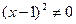 , получим
, получим
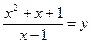 , тогда
, тогда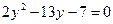
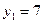 ;
; 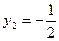
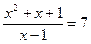 или
или 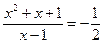
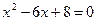
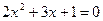
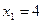 ;
; 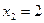
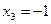 ;
; 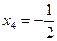
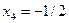
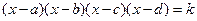 , где
, где 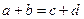 эффективно решать перемножением
эффективно решать перемножением 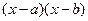 и
и 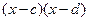 , а затем делать замену.
, а затем делать замену.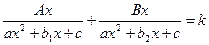 и в уравнениях к ним сводящимся, в знаменателях обоих дробей необходимо вынести х за скобки и сделать замену.
и в уравнениях к ним сводящимся, в знаменателях обоих дробей необходимо вынести х за скобки и сделать замену.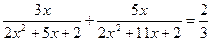 (1)
(1) 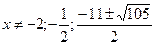
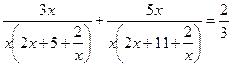 (2)
(2) область определения уравнения сузилась на
область определения уравнения сузилась на 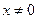 . Проверим, является ли
. Проверим, является ли  корнем уравнения. Не является.
корнем уравнения. Не является.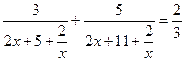
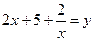 ,
, 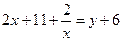 , тогда
, тогда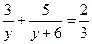
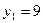 ;
; 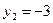
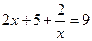 или
или 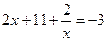
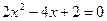
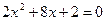
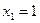

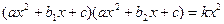 обе части уравнения делятся на
обе части уравнения делятся на 
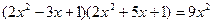
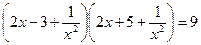
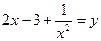 ;
; 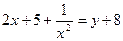 , тогда
, тогда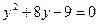
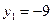 ;
; 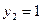
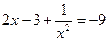 или
или 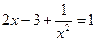
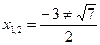
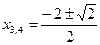
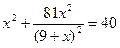
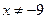
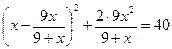
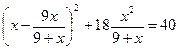
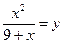 , тогда
, тогда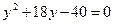
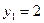 ;
; 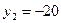
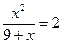 или
или 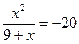
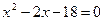
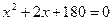
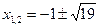 корней нет
корней нет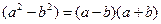
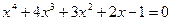
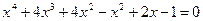
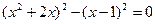
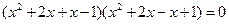
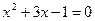 или
или 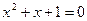
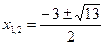 корней нет
корней нет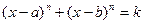 и к ним сводящиеся решаются при помощи замены
и к ним сводящиеся решаются при помощи замены 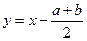
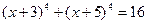
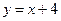 , тогда
, тогда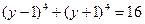
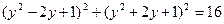
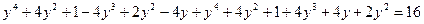
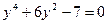
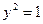 или
или 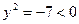 корней нет
корней нет ;
; 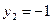
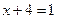 или
или 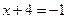
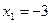
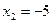
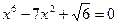
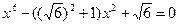
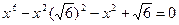
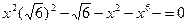
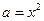
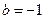
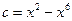
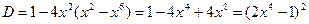
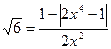 или
или 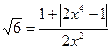
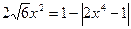
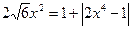

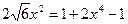
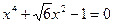
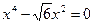
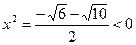 ;
;