Работа №3. Изучение динамики вращательного движения и измерение осевых моментов инерции твердых тел на маховике Обербека.
I. Измерение моментов инерции I0 крестовины без грузов
1. Определить массу m грузa P с подставкой (значения масс указаны на грузах). 2. Измерить штангенциркулем радиус шкива r. 3. Намотать нить на шкив и подвесить груз Р с подставкой на нить. Отпустив груз Р без толчка, измерить время его движения на пути h. 4. Вычислить линейное ускорение падающего груза по формуле (1). 5. Измерения, описанные в 3 и 4, проделать три раза с различными значениями высоты h. 6. Вычислить по формуле (6) момент инерции крестовины I 0 для каждого значения а. Найти среднее значение момента инерции I 0СР. 7. Рассчитать погрешность D I 0 определения I 0 как среднюю абсолютную погрешность по формуле D I 0 = Все результаты записать в таблицу, где рядом с обозначениями величин обязательно указать единицы их измерения.
Таблица
m = … кг; r = …. м; m 0 = … кг;
II. Измерение моментов инерции грузов
1. Четыре груза с одинаковой массой m 0 закрепить на концах спиц на одинаковых расстояниях R от центров грузов до оси вращения. Убедиться, что центр масс системы совпадает с осью вращения, т. е. система сбалансирована.
2. Записать значения m 0 и R в таблицу.
3. Выполнить измерения, описанные в пунктах 3 – 5 раздела I.
4. Вычислить момент инерции крестовины с грузами I для каждого значения а. Найти среднее значение I СР.
5. Рассчитать погрешность D I определения I как среднюю абсолютную погрешность по формуле D I = 6. Вычислить момент инерции грузов по формуле:
I Г = I СР - I 0СР. (9)
7. Определить погрешность D I Г определения момента инерции грузов по формуле: D I Г = D I + D I 0.
8. Записать окончательный результат в виде:
I = I Г ± D I Г.
9. Рассчитать величину момента инерции грузов по формуле (8) и сравнить с полученным в пункте 8 экспериментальным значением.
10. Грузы переместить на середину спиц и закрепить их. Измерить расстояние R от центров грузов до оси вращения. Описанным выше методом (см. пункты 3 – 9 раздела II) определить значения их момента инерции.
Контрольные вопросы 1. Сформулируйте основной закон динамики вращательного движения. 2. Напишите формулу пути при равноускоренном поступательном движении опускающегося груза. 3. Напишите формулу связи углового ускорения маховика с линейным ускорением опускающегося груза. 4. Проделайте вывод формулы для определения момента инерции грузов на спицах маховика на основании основного закона динамики вращательного движения. 5. Дайте определение момента инерции тела. 6. При каком положении грузов маховик Обербека раскручивается с наибольшим угловым ускорением? 7. Можно ли в данной лабораторной работе изменить момент силы, не меняя массу груза на нити? 8. Почему в том случае, когда грузы ближе к оси вращения, время движения меньше?
Список литературы
1. Савельев И.В. Курс общей физики: В 3-х т. Т. 1. М.: – Наука, 1987. 2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высш. шк., 2000. – С. 294. 3. Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006.
Работа №3. Изучение динамики вращательного движения и измерение осевых моментов инерции твердых тел на маховике Обербека.
Приборы и принадлежности. Маховик Обербека, автоматический счётчик времени, четыре цилиндрических тела с одинаковой массой, масштабная линейка.
Вращательным движением тела назывется такое движение, при котором все точки тела движутся по окружностям, плоскости которых параллельны друг другу, а центры лежат на одной прямой, называемой осью вращения. Для измерения осевого момента инерции, в работе используется крестообразный маховик Обербека.
Перемещая муфты вдоль стержней на то или иное расстояние r, можно изменять осевой момент инерции системы. Считая, что масса однородного цилиндра сосредоточена в его геометрическом центре, где размещён стопорный винт, выразим осевой момент инерции муфт по формуле
На оси маховика жёстко укреплены два соосных шкива различных диаметров d1 и d2, на которые в один ряд наматывается нить (нить считаем нерастяжимой и невесомой). Один конец нити прикрепляется к шкиву, к другому концу нити, переброшенной через вспомогательный блок 1, подвешивается груз массой m (4). Изменением массы груза m, путём наложения перегрузков с массой m1, можно изменять силу натяжения нити Т, под действием которой маховик совершает равномерно-ускоренное вращательное движение с угловым ускорением Одновременно под действием силы тяжести груз m совершает равноускоренное поступательное движение вниз. При этом считаем, что момент сил трения относительно оси вращения маховика мал по сравнению с моментом силы натяжения нити. На вертикальной стойке прибора укреплены два кронштейна: нижний (5) – неподвижный, верхний (3) – подвижный. Верхний кронштейн можно перемещать вдоль стойки и фиксировать в любом положении, задавая тем самым длину пути h вертикального перемещения груза m. Для измерения длины пути на стойке нанесена миллиметровая шкала. Прибор снабжён счётчиком времени – миллисекундомером, не ведущим отсчёт времени при нажатых кнопках «сеть» или «сброс». Измерения времени движения груза m осуществляется с использованием двух фотоэлектрических датчиков, вмонтированных в верхний и нижний кронштейны и подключенных к секундомеру. Расстояние между световыми лучами обоих датчиков равно длине пути вертикального перемещения груза h. Датчики включаются в работу при нажатии клавиши «сеть». Нажатие клавиши «пуск» включает секундомер и одновременно выключает электромагнит, удерживающий крестовину, после чего начинается вращение крестовины и движение груза m вниз. При пересечении грузом верхнего светового луча секундомер начинает отсчёт времени. При пересечении нижнего светового луча секундомер автоматически выключается. Время движения груза от одного светового луча до другого высвечивается на индикаторе секундомера с абсолютной ошибкой Расстояние Перед выполнением опытов на маховике Обербека необходимо добиться симметричного распределения грузов на крестовине. Это делается путём перемещения грузов 2 на противоположных стержнях так, чтобы при ненатянутой нити грузы оставались в состоянии безразличного равновесия. Для проведения опытов маховик приводят в равноускоренное вращательное движение, опуская груз m1 с заданной высоты и измеряя при этом время его движения t на пути h. Линейное ускорение движения груза можно вычислить по формуле
Так как при движении груза нить сматывается со шкива без проскальзывания, то линейное ускорение груза
(где С другой стороны согласно основному закону динамики вращательного движения (6) угловое ускорение (где Т – сила натяжения нити, d/2 - плечо силы). Согласно второму закону Ньютона действующая на нить сила
(где g – ускорение свободного падения, Поскольку нить не растяжима сила F, уравновешивается силой T. Следовательно, момент силы
Выразив из уравнения (6) (22). Как видно из (22), чтобы косвенно измерить момент инерции, надо прямыми измерениями найти массу груза, создающего натяжение нити, диаметр блока, по которому движется точка приложения силы, высота с которой опускается груз, и время опускания. Вычисленное по формуле (22) значение момента инерции маховика
Искомый момент инерции грузов
где
Осевой момент инерции маховика без грузов Считая грузы материальными точками, можно рассчитать теоретическое значение осевого момента инерции по формуле (16):
(где m – масса одного вращающегося груза 2, r – расстояние центра масс груза от оси вращения). Сопоставление значений моментов инерции четырёх вращающихся грузов, рассчитанных по формулам (23) и (24) позволяет судить о качестве проделанной работы. Проделав косвенные измерения момента инерции груза
|

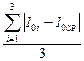 ,
,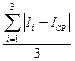 ,
, Цель работы. Усвоить основной закон динамики вращательного движения. Косвенно измерить момент инерции цилиндрических тел. Установить зависимость осевых моментов инерции вращающихся на маховике грузов от расстояния до оси вращения.
Цель работы. Усвоить основной закон динамики вращательного движения. Косвенно измерить момент инерции цилиндрических тел. Установить зависимость осевых моментов инерции вращающихся на маховике грузов от расстояния до оси вращения.
 Маховик Обербека (рис. 3) представляет собой свободно вращающуюся относительно неподвижной горизонтальной оси крестовину, выполненную в виде четырёх взаимно перпендикулярных металлических стержней. Ось крестовины закреплена на вертикальной стойке, установленной на массивном основании. На стержни одеты цилиндрические муфты (2) известной массы, которые закрепляются на заданном расстоянии r от оси вращения с помощью стопорных винтов.
Маховик Обербека (рис. 3) представляет собой свободно вращающуюся относительно неподвижной горизонтальной оси крестовину, выполненную в виде четырёх взаимно перпендикулярных металлических стержней. Ось крестовины закреплена на вертикальной стойке, установленной на массивном основании. На стержни одеты цилиндрические муфты (2) известной массы, которые закрепляются на заданном расстоянии r от оси вращения с помощью стопорных винтов.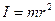 (17).
(17).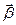 , которое согласно основному закону динамики вращательного движения (6) прямо пропорционально моменту силы натяжения нити
, которое согласно основному закону динамики вращательного движения (6) прямо пропорционально моменту силы натяжения нити 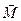 . Поскольку сила натяжения направлена вертикально, её плечо в соответствии с (3) равно
. Поскольку сила натяжения направлена вертикально, её плечо в соответствии с (3) равно 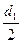 или
или 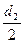 .
. , что намного меньше точности измерения времени человеком-оператором.
, что намного меньше точности измерения времени человеком-оператором.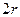 между центрами масс, противоположно закреплённых грузов, измеряются мерной линейкой. Диаметры шкивов измеряются штангенциркулем. Массы грузов 4 заданы с абсолютной погрешностью
между центрами масс, противоположно закреплённых грузов, измеряются мерной линейкой. Диаметры шкивов измеряются штангенциркулем. Массы грузов 4 заданы с абсолютной погрешностью 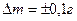 .
. (18).
(18).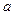 равно касательному ускорению точек, лежащих на цилиндрической поверхности шкива. Следовательно, угловое ускорение маховика
равно касательному ускорению точек, лежащих на цилиндрической поверхности шкива. Следовательно, угловое ускорение маховика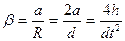 (19)
(19)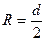 - радиус шкива).
- радиус шкива). . Момент силы
. Момент силы 
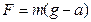 (20),
(20),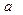 - линейное ускорение поступательного движения груза).
- линейное ускорение поступательного движения груза).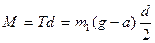 (21).
(21).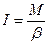 и подставив в эту формулу
и подставив в эту формулу 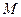 и
и 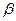 из (18) и (20) получим:
из (18) и (20) получим: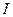 включает в себя момент инерции крестовины с блоком
включает в себя момент инерции крестовины с блоком 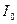 и момент инерции четырёх грузов
и момент инерции четырёх грузов 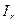 с массой m (2):
с массой m (2):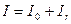 (23).
(23). (24),
(24),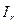 - осевой момент инерции вращающихся грузов 2;
- осевой момент инерции вращающихся грузов 2;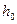 и
и 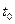 , измеренные при вращении крестовины со снятыми с неё грузами.
, измеренные при вращении крестовины со снятыми с неё грузами.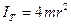 (25),
(25), их центров от оси вращения (поочерёдно размещая грузы 2 на концах стержней, на их середине и вблизи оси крестовины), можно опытным путём установить характер зависимости момента инерции от распределения массы относительно оси вращения. По определению момента инерции, как меры инертности тела при вращательном движении, эта зависимость является квадратичной (5). Графиком такой зависимости является парабола
их центров от оси вращения (поочерёдно размещая грузы 2 на концах стержней, на их середине и вблизи оси крестовины), можно опытным путём установить характер зависимости момента инерции от распределения массы относительно оси вращения. По определению момента инерции, как меры инертности тела при вращательном движении, эта зависимость является квадратичной (5). Графиком такой зависимости является парабола  . Откладывая на оси
. Откладывая на оси 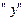 значения моментов инерции, рассчитанных по формулам (23) и (24), а по оси
значения моментов инерции, рассчитанных по формулам (23) и (24), а по оси  квадрат расстояния
квадрат расстояния  , можно построить экспериментальные и теоретические параболы. При этом принимать коэффициент
, можно построить экспериментальные и теоретические параболы. При этом принимать коэффициент 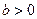 равным массе 4-х грузов (
равным массе 4-х грузов (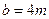 ). Совмещение точек таких парабол служит подтверждением качества выполнения эксперимента и правомерности применения модели материальных точек к однородным цилиндрам равной длины.
). Совмещение точек таких парабол служит подтверждением качества выполнения эксперимента и правомерности применения модели материальных точек к однородным цилиндрам равной длины.


