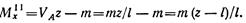Решение. При построении эпюр для балок с одним защемленным концом можно не определять опорные реакции
При построении эпюр для балок с одним защемленным концом можно не определять опорные реакции. Проводя сечение, будем рассматривать равновесие той части, к которой приложены только внешние (активные) силы. Для балки по рис. 2.50, а такой частью будет левая. Рассматривая равновесие левой отсеченной части балки, выразим поперечную силу и изгибающий момент в произвольном сечении
Поперечная сила положительна, так как внешняя нагрузка направлена слева от сечения вверх, Qy постоянна на всем протяжении балки. Эпюра поперечных сил построена на рис. 2.50, б.
Оба слагаемых, входящих в выражение изгибающего момента, положительны, так как соответствующие внешние силы изгибают балку выпуклостью вниз. Изгибающий момент выражается линейной функцией от абсциссы сечения z. Поэтому для построения этой эпюры достаточно найти значения изгибающего момента только в двух сечениях балки:
Эпюра моментов показана на рис. 2.50, в.
Пример 2. Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 2.52, а.
Определяем опорные реакции. Реакция V А направлена вверх, VB — вниз, так как эти реакции образуют пару сил, уравновешивающую пару с моментом т. Составляя суммы моментов относительно опорных точек Л и В, находим:
Для проверки опорных реакций составляем сумму проекций на вертикальную ось:
следовательно, реакции вычислены правильно. Балка имеет два участка I, II. Проводим произвольное сечение на участке I на расстоянии z от опоры А и рассматриваем левую отсеченную часть. Поперечная сила на этом участке постоянна, равна реакции VА и положительна, так как эта реакция направлена вверх и приложена слева от сечения.
Изгибающий момент в произвольном сечении участка I
Момент положителен, так как сила VA изгибает балку выпуклостью вниз. В произвольном сечении участка II поперечная сила будет такой же, как на участке I:
Изгибающий момент в произвольном сечении участка II
Вычислим изгибающий момент в начале и в конце участка II:
Эпюры Qy и Мх показаны на рис. 2.52, б, в. В сечении, где приложен сосредоточенный момент,в эпюре изгибающих моментов имеется скачок, равный по величине внешнему моменту. Пример 3. Для балки, изображенной на рис. 2.53, а, построить эпюры Qy и Мг.
|

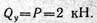


 Решение
Решение