Светодиодная лента SNT 60 LED 3528 белая холодная IP65 влагозащищенная 3 страница
48. ↑; Wehling T. O. et. al. Molecular Doping of Graphene Nano Lett. 8, 173 (2008)DOI:10.1021/nl072364w 49. ↑; S.R.C.Vivekchand; Chandra Sekhar Rout, K.S.Subrahmanyam, A.Govindaraj and C.N.R.Rao (2008). «Graphene-based electrochemical supercapacitors». J. Chem. Sci., Indian Academy of Sciences 120, January 2008: 9−13. 50. ↑; Piotr Matyba, Hisato Yamaguchi, Goki Eda, Manish Chhowalla, Ludvig Edman, Nathaniel D. Robinson. Graphene and Mobile Ions: The Key to All-Plastic, Solution-Processed Light-Emitting Devices (англ.) // Журнал ACS Nano. — American Chemical Society, 2010. — В. 4 (2). — С. 637—642. — DOI:10.1021/nn9018569 51. ↑; Предложена схема двумерного метаматериала на основе графена 52. ↑; Ando T. Screening Effect and Impurity Scattering in Monolayer Graphene J. Phys. Soc. Jpn. 75, 074716 (2006) DOI:10.1143/JPSJ.75.074716 53. ↑; Hatsugai Y. cond-mat/0701431 54. ↑; Gusynin V. P., et. al. AC conductivity of graphene: from tight-binding model to 2+1-dimensional quantum electrodynamics Int. J. Mod. Phys. B 21, 4611 (2007)DOI:10.1142/S0217979207038022 55. ↑; Katsnelson M. I. et al., Chiral tunnelling and the Klein paradox in graphene Nat. Phys. 2, 620 (2006) DOI:10.1038/nphys384 56. ↑; Cheianov V. V. and Fal’ko V. I., Selective transmission of Dirac electrons and ballistic magnetoresistance of n-p junctions in graphene Phys. Rev. B 74, 041403 (2006)DOI:10.1103/PhysRevB.74.041403 57. ↑; Trauzettel B. et al., Spin qubits in graphene quantum dots Nat. Phys. 3, 192 (2007)DOI:10.1038/nphys544 58. ↑; Silvestrov P. G. and Efetov K. B. Quantum Dots in Graphene Phys. Rev. Lett. 98, 016802 (2007) DOI:10.1103/PhysRevLett.98.016802 59. ↑; Geim A. K., Novoselov K. S. The rise of graphene. Nat. Mat. 6, 183 (2007).DOI:10.1038/nmat1849 60. ↑; Bordag M., Fialkovsky I. V., Gitman D. M., Vassilevich D. V. (2009). «Casimir interaction between a perfect conductor and graphene described by the Dirac model». Physical Review B 80. DOI:10.1103/PhysRevB.80.245406. 61. ↑; Fialkovsky I. V., Marachevskiy V.N., Vassilevich D. V. (2011). «Finite temperature Casimir effect for graphene». 62. ↑; Hwang E. H. et al., Carrier Transport in Two-Dimensional Graphene Layers Phys. Rev. Lett. 98, 186806 (2007) DOI:10.1103/PhysRevLett.98.186806 cond-mat 63. ↑; Bolotin K. I. et. al. Ultrahigh electron mobility in suspended graphene Solid State Comm. 146, 351 (2008) DOI:doi:10.1016/j.ssc.2008.02.024[Ошибка: Неверный DOI!]препринт 64. ↑; Moser J. et. al. Current-induced cleaning of graphene Appl. Phys. Lett. 91, 163513 (2007) DOI:10.1063/1.2789673 65. ↑; David Nelson (Editor), Steven Weinberg (Editor), T. Piran (Editor) „Statistical Mechanics of Membranes and Surfaces“. — 2nd ed. — World Scientific, Singapore. — p. 444 с. — ISBN 978-981-238-760-8. 66. ↑; Meyer J. C. et. al. The structure of suspended graphene sheets Nature 446, 60 (2007) DOI:10.1038/nature05545 67. ↑; Bunch J. S. et al., Electromechanical Resonators from Graphene Sheets Science 315, 490 (2007) DOI:10.1126/science.1136836 68. ↑; Ludwig A. W. W., et al., «Integer quantum Hall transition: An alternative approach and exact results» Phys. Rev. B 50, 7526 (1994) DOI:10.1103/PhysRevB.50.7526; Ziegler K., «Scaling behavior and universality near the quantum Hall transition» Phys. Rev. B 55, 10661 (1997) DOI:10.1103/PhysRevB.55.10661; Ziegler K., «Delocalization of 2D Dirac Fermions: The Role of a Broken Supersymmetry» Phys. Rev. Lett. 80, 3113 (1998) DOI:10.1103/PhysRevLett.80.3113; Katsnelson M. I., «Zitterbewegung, chirality, and minimal conductivity in graphene» Eur. Phys. J. B 51, 157 (2006) DOI:10.1140/epjb/e2006-00203-1; Tworzydlo J. et al., «Sub-Poissonian Shot Noise in Graphene» Phys. Rev. Lett. 96, 246802 (2006)DOI:10.1103/PhysRevLett.96.246802; Cserti J. «Minimal longitudinal dc conductivity of perfect bilayer grapheme» Phys. Rev. B 75, 033405 (2007)DOI:10.1103/PhysRevB.75.033405; Ziegler K., «Robust Transport Properties in Graphene» Phys. Rev. Lett. 97, 266802 (2006) DOI:10.1103/PhysRevLett.97.266802 69. ↑ Перейти к: 12 Peres N. M. R., et. al. Electronic properties of disordered two-dimensional carbon Phys. Rev. B 73, 125411 (2006) DOI:10.1103/PhysRevB.73.125411 70. ↑ Перейти к: 12 Gusynin V. P. et al. «Unconventional Integer Quantum Hall Effect in Graphene» Phys. Rev. Lett. 95, 146801 (2005) DOI:10.1103/PhysRevLett.95.146801 71. ↑ Перейти к: 12 Novoselov K. S., Jiang Z., Zhang Y, Morozov S. V., Stormer H. L., Zeitler U., Maan J. C., Boebinger G. S., Kim P., Geim1 A. K. Room-Temperature Quantum Hall Effect in Graphene (англ.) // Science. — 2007. — Т. 315. — С. 1379. —DOI:10.1126/science.1137201 72. ↑; Novoselov K. S., McCann E., Morozov S. V., Fal'ko V. I., Katsnelson M. I., Zeitler U., Jiang D., Schedin F., Geim A. K. Unconventional quantum Hall effect and Berry's phase of 2in bilayer graphene (англ.) // Nature Physics. — 2006. — Т. 2. — С. 177—180. —DOI:10.1038/nphys245 — arΧiv: cond-mat/0602565 73. ↑; Katsnelson, 2012, с. 17 74. ↑; A. Castro Neto et al. Drawing conclusions from graphene Phys. World 19 (11), p 33 (2006) ISSN 0953-8585. 75. ↑; Sharapov S. G. et al. «Magnetic oscillations in planar systems with the Dirac-like spectrum of quasiparticle excitations» Phys. Rev. B 69, 075104 (2004)DOI:10.1103/PhysRevB.69.075104. 76. ↑; R. Saito, G. Dresselhaus, M. S. Dresselhaus. „Physical Properties of Carbon Nanotubes“. — World Scientific. — p. 272 с. — ISBN 1-86094-223-7. 77. ↑; Dahal H. P. et al. «Absence of Wigner crystallization in graphene» Phys. Rev. B 74, 233405 (2006) DOI:10.1103/PhysRevB.74.233405 78. ↑; Pisana S. et. al. Breakdown of the adiabatic Born-Oppenheimer approximation in graphene Nature Materials 6, 198 (2007) DOI:10.1038/nmat1846 79. ↑; Микросхемы из графена смогут охлаждать сами себя 80. ↑; Self-cooling observed in graphene electronics | News Bureau | University of Illinois 81. ↑; Нобелевские лауреаты обнаружили «жидкокристаллические» электроны 82. ↑; Catharine Paddock PhD. Graphene shows anticancer potential (англ.). Medical News Today (26 February 2015). Проверено 23 марта 2015. 83. ↑; ГРАФЕН ДЕМОНСТРИРУЕТ ПРОТИВООПУХОЛЕВЫЙ ПОТЕНЦИАЛ (рус.).Проверено 23 марта 2015. Литература[править | править вики-текст] · Katsnelson M. I. Graphene: Carbon in Two Dimensions. — New York: Cambridge University Press, 2012. — 366 p. — ISBN 978-0-521-19540-9. · Warner J. H., Schäffel F., Bachmatiuk A., Rümmeli M. H. Graphene: Fundamentals and emergent applications. — Elsevier, 2013. — 470 p. — ISBN 978-0-12-394593-8. · Новосёлов К. С. Графен: материалы Флатландии // УФН. — 2011. — Т. 181. — С. 1299—1311. — DOI:10.3367/UFNr.0181.201112f.1299 · Гейм А. К. Случайные блуждания: непредсказуемый путь к графену // УФН. — 2011. — Т. 181. — С. 1284—1298. —DOI:10.3367/UFNr.0181.201112e.1284 · Елецкий А. В., Искандарова И. М., Книжник А. А., Красиков Д. Н. Графен: методы получения и теплофизические свойства // УФН. — 2011. — Т. 181. — С. 227—258. — DOI:10.3367/UFNr.0181.201103a.0233 · Сорокин П. Б., Чернозатонский Л. А. Полупроводниковые наноструктуры на основе графена // УФН. — 2013. — Т. 183. — С. 113–132. —DOI:10.3367/UFNr.0183.201302a.0113 · Gusynin V. P., Sharapov S. G., Carbotte J. P. AC conductivity of graphene: from tight-binding model to 2+1-dimensional quantum electrodynamics (англ.) // Int. J. Mod. Phys. B. — 2007. — Т. 21. — С. 4611. — DOI:10.1142/S0217979207038022 — arΧiv: 0706.3016 · Castro Neto A. H., Guinea F., Peres N. M. R., Novoselov K. S., Geim A. K. Электронные свойства графена (англ.) = The electronic properties of graphene // Rev. Mod. Phys. — 2009. — Т. 81. — С. 109—162. — DOI:10.1103/RevModPhys.81.109 — arΧiv: 0709.1163 · Zhu Y., Murali S., Cai W., Li X., Suk J. W., Potts J. R., Ruoff R. S. Graphene and Graphene Oxide: Synthesis, Properties, and Applications (англ.) // Adv. Mater.. — 2010. — Т. 22. — С. 3906—3924. — DOI:10.1002/adma.201001068 · Meyer J. C., Geim A. K., Katsnelson M. I., Novoselov K. S., Booth T. J., Roth S. Структура подвешенных графеновых листов (англ.) = The structure of suspended graphene sheets // Nature. — 2007. — Т. 446. — С. 60—63. — DOI:10.1038/nature05545 — arΧiv: cond-mat/0701379 · Novoselov K. S., Geim A. K., Morozov S. V., Jiang D., Zhang Y., Dubonos S. V., Grigorieva I. V., Firsov A. A. Эффект поля в атомарно тонких углеродных плёнках (англ.) = Electric Field Effect in Atomically Thin Carbon Films // Science. — 2004. — Т. 306. — С. 666—669. — DOI:10.1126/science.1102896 —arΧiv: cond-mat/0410550 · Novoselov K. S., Jiang D., Schedin F., Booth T. J., Khotkevich V. V., Morozov S. V., Geim A. K. Двумерные атомные кристаллы (англ.) = Two-dimensional atomic crystals // Proc. Nat. Acad. Sci. U.S.A.. — 2005. — Т. 102. — С. 10451—10453. — DOI:10.1073/pnas.0502848102 · Novoselov K. S., Geim A. K., Morozov S. V., Jiang D., Katsnelson M. I., Grigorieva I. V., Dubonos S. V., Firsov A. A. Двумерный газ безмассовых фермионов Дирака в графене (англ.) = Two-dimensional gas of massless Dirac fermions in graphene // Nature. — 2005. — Т. 438. — С. 197—200. —DOI:10.1038/nature04233 — arΧiv: cond-mat/0509330 · Geim A. K., Novoselov K. S. Восход графена (англ.) = The rise of graphene // Nature Materials. — 2007. — Т. 6. — С. 183—191. —DOI:10.1038/nmat1849 — arΧiv: cond-mat/0702595 · Elias D. C., Nair R. R., Mohiuddin T. M. G., Morozov S. V., Blake P., Halsall M. P., Ferrari A. C., Boukhvalov D. W., Katsnelson M. I., Geim A. K., Novoselov K. S. Управление свойствами графена с помощью обратимой гидрогенизации: свидетельство в пользу графана (англ.) = Control of Graphene's Properties by Reversible Hydrogenation: Evidence for Graphane // Science. — 2009. — Т. 323. — С. 610—613. — DOI:10.1126/science.1167130 — arΧiv: 0810.4706 · Malard L. M., Pimenta M. A., Dresselhaus G., Dresselhaus M. S. Рамановская спектроскопия графена (англ.) = Raman spectroscopy in graphene // Physics Reports. — 2009. — Т. 473. — С. 51—87. — DOI:10.1016/j.physrep.2009.02.003 · Li X., Cai W., An J., Kim S., Nah J., Yang D., Piner R., Velamakanni A., Jung I., Tutuc E., Banerjee S. K., Colombo L., Ruoff R. S. Синтез высококачественных и однородных графеновых плёнок большой площади на медных фольгах (англ.) = Large-Area Synthesis of High-Quality and Uniform Graphene Films on Copper Foils // Science. — 2009. — Т. 324. — С. 1312—1314. — DOI:10.1126/science.1171245 · Bae S., Kim H., Lee Y., Xu X., Park J., Zheng Y., Balakrishnan J., Lei T., Kim H. R., Song Y. I., Kim Y., Kim K. S., Özyilmaz B., Ahn J., Hong B. H., Iijima S. Рулонное производство 30-дюймовых графеновых плёнок для прозрачных электродов (англ.) = Roll-to-roll production of 30-inch graphene films for transparent electrodes // Nat. Nanotech.. — 2010. — Т. 5. — С. 574—578. — DOI:10.1038/nnano.2010.132 · Berger C., Song Z., Li X., Wu X., Brown N., Naud C., Mayou D., Li T., Hass J., Marchenkov A. N., Conrad E. H., First P. N., de Heer W. A. Электронный конфайнмент и когерентность в эпитаксиальном графене (англ.) = Electronic Confinement and Coherence in Patterned Epitaxial Graphene // Science. — 2006. — Т. 312. — С. 1191—1196. — DOI:10.1126/science.1125925 · Kotov V. N., Uchoa B., Pereira V. M., Guinea F., Castro Neto A. H. Электрон — электронные взаимодействия в графене: настоящее состояние и перспективы (англ.) = Electron-Electron Interactions in Graphene: Current Status and Perspectives // Rev. Mod. Phys.. — 2012. — Т. 84. — С. 1067—1125. —DOI:10.1103/RevModPhys.84.1067 — arΧiv: 1012.3484 · Abergel D. S. L., Apalkov V., Berashevich J., Ziegler K., Chakraborty T. Свойства графена: теоретическая перспектива (англ.) = Properties of graphene: a theoretical perspective // Adv. Phys.. — 2010. — Т. 59. — С. 261—482. — DOI:10.1080/00018732.2010.487978 — arΧiv: 1003.0391 · Das Sarma S., Adam S., Hwang E. H., Rossi E. Свойства графена: теоретическая перспектива (англ.) = Electronic transport in two dimensional graphene // Rev. Mod. Phys.. — 2011. — Т. 83. — С. 407—470. — DOI:10.1103/RevModPhys.83.407 — arΧiv: 1003.4731 · Cooper D. R., D’Anjou B., Ghattamaneni N., Harack B., Hilke M., Horth A., Majlis N., Massicotte M., Vandsburger L., Whiteway E., Yu V. Экспериментальный обзор по графену (англ.) = Experimental Review of Graphene // ISRN Condensed Matter Physics. — 2012. — С. 501686. — DOI:10.5402/2012/501686 —arΧiv: 1110.6557 · Andrei E. Y., Li G., Du X. Электронные свойства графена: взгляд со стороны сканирующей туннельной микроскопии и магнетотранспорта (англ.) = Electronic properties of graphene: a perspective from scanning tunneling microscopy and magnetotransport // Rep. Prog. Phys.. — 2012. — Т. 75. — С. 056501. — DOI:10.1088/0034-4885/75/5/056501 — arΧiv: 1204.4532 · Shen H., Zhang L., Liu M., Zhang Z. Биологические и медицинские применения графена (англ.) = Biomedical Applications of Graphene // Theranostics. — 2012. — Т. 2. — С. 283—294. — DOI:10.7150/thno.3642 · Schwierz F. Графеновые транзисторы (англ.) = Graphene transistors // Nat. Nanotech.. — 2010. — Т. 5. — С. 487—496. — DOI:10.1038/nnano.2010.89 · Bonaccorso F., Sun Z., Hasan T., Ferrari A. C. Графеновая фотоника и оптоэлектроника (англ.) = Graphene photonics and optoelectronics // Nat. Photon.. — 2010. — Т. 4. — С. 611—622. — DOI:10.1038/nphoton.2010.186 · Pumera M. Графен как биосенсор (англ.) = Graphene in biosensing // Materials Today. — 2011. — Т. 14. — С. 308—315. — DOI:10.1016/S1369-7021(11)70160-2 · Avouris P. Графен: электронные и фотонные свойства и приборы (англ.) = Graphene: Electronic and Photonic Properties and Devices // Nano Lett.. — 2010. — Т. 10. — С. 4285—4294. — DOI:10.1021/nl102824h · Лозовик Ю. Е., С.П. Меркулова, А.А. Соколик Коллективные электронные явления в графене // УФН. — 2008. — Т. 178. — № 7. — С. 757–776. Ссылки[править | править вики-текст] · Галерея фотографий графита и графена (англ.) · Графен: ЦЕРН на столе — лекция, прочитанная М. Кацнельсоном в 2010 г. при поддержке фонда Династия. Лаборатории [править | править вики-текст] · Condensed Matter Physics Group (англ.). The University of Manchester. Проверено 28 октября 2012. Архивировано из первоисточника 20 января 2013. · Kim Group Home page (англ.). Columbia University. Проверено 28 октября 2012. Архивировано из первоисточника 20 января 2013. · Andrei Group (англ.). Rutgers, The State University of New Jersey. Проверено 28 октября 2012. Архивировано из первоисточника 20 января 2013. · Nanomaterials and Spectroscopy Group (англ.). University of Cambridge. Проверено 28 октября 2012. Архивировано из первоисточника 20 января 2013.
Спирометрия тыныс алу әдісін өлшейтін әдіс. Графикалык жолмен зерттеу әдіс нәтижелерін тіркеу аркылы алынған графикалык сызыкты спирограмма деп атайды. Спирограммада абцисса осіне уакыт, ал ординатаға ауа көлемі салынады. Тыныс алу кезінде өкпе бронх жүйесіндегі ауа көлемі өзгереді. Бұл өзгерістерді спирометриялык кондыргы тіркеп спирограмма түрінде береді.Спирометрді қосқаннан кейін оның экранында дәрігерге қаралушы туралы мәліметтерді енгізетін мәзір шығады. Егер қоршаған ортаның күйі бөлменің температурасы ауаның қысымы спирометрдің орны өзгермесе онда дәрігерге қаралушы туралы мәліметтерді енгізіп зерттеуді жүргізу керек. 60. Сұйықтың тұтқырлығы ушін Нютон теңдеуі. F=ndv/dx.S мұндағы dv/dx жылдамдык градиенті, ол жылдамдыктың белгілі бағыттағыбірлік ұзындығына сәйкес келетін шамаға т ең; S әсерлесуші қабат ауданы, n тұтқырлық коэффициенті немесе динамикалық тұтқырлық. Динамикалық тұтқырлық СИ жуйесінде Паскал.c Өлшенеді.
57. Сұйықтың беттік керілу құбылысы молекула аралық әсерлесулерден пайда болады. Оны сұйықтың түбінде және беткі қабатында орналасқан молекулаларға әсер ететін күштердің пайда болуынан білеміз.Егер молекула сұйықтың терең қабатында орналасқан болса, оған, оны қоршаған молекулалар тарапынан әсер ететін қорытқыF куші нолге тең болады. Егер молекула сұйықтың беткі қабатында орналасқан болса онда оған жоғарғы жағынан қоршаған ауа, яғни газ молекулалары тарапынан әсер ететін күштің шамасынан, сұйық молекулалары тарапынан әсер ететін тарту күшінің шамасы басым болады. Яғни F қорытқы куш нолге тең болмайды. Бұл күш молекуланы сұйықтың беткі қабатынан төменге қарай тартуға тырысады. Осы кушті сан жағынан сипаттау үшін беттік керілу коэффициенті деген шама енгізіледі. Сұйықтың терең қабатындагы молекуланы беткі қабатқа шығару үшін F күшке қарсы А жұмысын атқару керек. Беттік қабаттың бірлік ауданына сәйкес келетін осы жұмыстың шамасын 6=dA/dS беттік керілу коэффициенті деп атайды. Ол сұйықтыңеркін бетінің бірлік ауданына сәйкес келетін W беттік энергия шамасына саан жағынан тең 58.Сұйықтықтың беттік керілу коэффиценті және оны өлшеу. Сұйықтың беттік керілу құбылысы молекула аралық әсерлесулерден пайда болады. Оны сұйықтың түбінде және беткі қабатында орналасқан молекулаларға әсер ететін күштердің пайда болу табиғатынан байқауға болады.Егер молекула сұйықтың терең қабатында орналасқан болса (2-сурет), оған, оны қоршаған молекулалар тарапынан әсер ететін қорытқы F күші нөлге тең болады. Егер молекула сұйықтың беткі қабатында орналасқан болса (3-сурет), онда оған жоғарғы жағынан қоршаған ауа, яғни газ молекулалары тарапынан әсер ететін күштың шамасынан, сұйық молекулалары тарапынан әсер ететін тарту күшінің шамасы басым болады. Яғни F қорытқы күш нөлге тең болмайды. Бұл күш молекуланы сұйықтың беткі қабатынан төменге (ішке) қарай тартуға тырысады. Осы күшті сан жағынан сипаттау үшін σ; беттік керілу коэффициенті деген шама енгізіледіСұйықтың терең қабатындағы молекуланы беткi қабатқа шығару үшiн F күшке қарсы A жұмысын атқару керек. Беттiк қабаттың бiрлiк ауданына сәйкес келетiн осы жұмыстың шамасын s = dA/dS беттiк керiлу коэффициентi деп атайды. Ол сұйықтың еркiн бетiнiң бiрлiк ауданына сәйкес келетiн W беттiк энергия шамасына сан жағынан тең болады, яғни s = dW/dS. 59 Сұйықтықтың тұтқырлығы немесе ішкі үйкеліс сұйыктың ағуы кезінде байкалатын басты құбылыстың бірі. Түтікпен аққан сұйықтың молекулалары тутік қабырғасымен әсерлеседі, соның нәтижесінде сұйықтың түтік қабырғасына жанасқан қабатының ағу жылдамдығы төмендейді., бұл қабат өз кезегінде келесі қабаттың ағу қозғалысын тежейді, ол келесі қабатқа әсер етеді, осылайша жалғаса береді. Түтіктің осіне жақындаған сайын бұл құбылыстың әсері төмендеп, түтік осі бойындағы сұйық ағысы жылдамдығын сақтайды. Сонымен қозғалыстағы сұйықтардың қабаттары арасында ішкі үйкеліс болады екен., оны тұтқырлық дейді. Осы күш әсерінен түтіктің көлденең қимасындағы сұйықтардың ағу жылдамдықтары әр түрлі болады, түтіктің осі бойымен ағатын сұйық жылдамдығы төмен мәнге ие болады. V1<v2<v3<v4 60. Сұйықтың тұтқырлығы ушін Нютон теңдеуі. F=ndv/dx.S мұндағы dv/dx жылдамдык градиенті, ол жылдамдыктың белгілі бағыттағыбірлік ұзындығына сәйкес келетін шамаға т ең; S әсерлесуші қабат ауданы, n тұтқырлық коэффициенті немесе динамикалық тұтқырлық. Динамикалық тұтқырлық СИ жуйесінде Паскал.c Өлшенеді 61.Ньютондық сұйықтықтар. Ньютон заңына бағынатын сұйықтарды ньютондық сұйықтар деп атайды. Мұндай сұйқтардың тұтқырлық коэффициенттері сұйықтың құрылымына, оның температурасы мен қысымына тәуелді, ал жылдамдық градиентіне тәуелсіз болады. Көптеген сұйықтар, мысалы су, түрлі ертінділер, төменгі молекулалы органикалық сұйықтар, барлық газдар ньютондық сұйықтарға жатады. 360С температурадағы қанның тұтқырлық коэффициенті 4-6∙10-3 Па∙с тең, ауыр жұмыстар кезінде тұтқырлық коэффициенті жоғарылайды, сондай-ақ тұтқырлықтың шамасына кей ауру түрлері де әсер етеді, мысалы, қан диабеті кезінде қан тұтқырлығы 23∙10-3 Па∙с дейін жоғарылайды, ал туберкулез кезінде керісінше 1∙10-3 Па∙с дейін төмендейді.
62.Ламинарлы және турбулентті ағыс. Сұйықты ағыс түріне байланысты ламинарлы және турбулентті деген түрлерге бөлінеді. Ламинарлы деп аққан сұйық қабаттары бір бірімен араласпайтын, бір қабат екінші қабат бетімен сырғи ағатын ағысты атайды. Мұндай ағыстың жылдамдығы барлық қабаттарда бірдей мәңге ие болады. Егер сұйықтың ағу жылдамдығы белгілі бір шамадан асса, онда сұйық қабаттары бір бірімен араласып, сұйық бөлшектерінің ағу траекториялыры күрделеніп, ағыс құйын тәрізді болады, мұндай ағыс турбулентті деп аталынады. Егер аққан сұйық қабаттарының жылдамдықтарының айырмашылығы белгілі бір шамадан асса, онда қабаттардағы қысым өзгереді, нәтижесінде сұйық бөлшектері қысым шамасы үлкен сыртқы қабаттан, қысымы төмен ішкі қабатқа қаарй ауысады, мұндай орын ауыстырулар ағыстың турбулентті болуына және ағыстың дыбыс шығаруына алып келеді. (турбуленті ағыстың мед маңызы: өкпе шуы, жүрек клапаны, Коротков әдісі). 63.Турбулентті ағысты медицинада қолдану. Сұйық ағысының ламинарлыдан ағыстан турбулентті ағысқа ауысуына сәйкес келетін жылдамдық шамасын кризистік vкр жылдамдық деп атайды және оның сан мәнін Рейнольдс саны арқылы анықталады, бұл шама ағыстың түрін сипаттайды және өлшем бірліксіз болып келеді. Рейнольдс саны деп Re= Dvr/h өрнегімен анықталынатын шаманы атайды, мұндағы v- сұық ағысының жылдамдығы, r және h- сұйықтың тығыздығы мен тұтқырлығы, D- ағыстың берілген жағдайдағы кедергісін сипататйтын шама (мысалы, осы жағдайда түтік диаметрі). Шын мәнінде ағыстың ламинарлыдан турбулентке өтетуін сипаттайтын Рейнольдс санын эксперимент арқылы анықтайды. Мысалы, іші жылтыр, цилиндр түтік ішінде аққан су үшін бұл шама Re=2300 тең. 64.Сұйықтың көлемдік және сызықтық жылдамдығы. Сұйықтың ағу жылдамдығы көлемдік және сызықтық; деген шамалармен сипатталады. Көлемдік жылдамдық Q деп, бірлік уақыт ішінде түтік арқылы ағып өткен сұйықтың V көлемін атайды: Q = V/t, бұл шама мл/с, л/мин және т.б. өлшенеді. Сызықтық жылдамдық v деп, сұйықтың бірлік уақыт ішінде ағып өткен жолының ұзындығын атайды: v =L/t. Көлемдік және сызықтық жылдамдықтар мына түрде өз ара тәуелді: Q = v× S, мұндағы S- аққан сұйықтың көлденең қимасы. 65-66.Сұйық ағысының үздіксіздік теңдеуі. Түтік арқылы ағып жатқан біртұтас сұйық үшін мына ереже орындалады: түтіктің кез келген көлденең қимасы арқылы бірлік уақыт ішінде бірдей көлемде сұйық ағып өтеді: Q =v×S = const, бұл өрнекті сұйық ағысының үздіксіздік теңдеуі деп атайды. Мұнан v1 ×S1 = v2×S2 немесе S1/S2 = v2/v1 тең: аққан сұйықтың көлденең қимасы үлкен болған сайын, оның жылдамдығы төмен болады. S2> S1> S3 мұнан v3> v2> v1 Сұйық ағыны үшін Пуайзель теңдеуі. Q = (p1 –p2)pR4/8hL.Бұл өрнек Пуазейль формуласы деп аталады. Өрнектегі
|

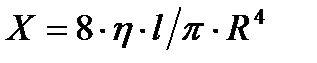 шама гидравликалық кедергі деп аталады, сонда Пуазейля формуласы мына түрге келеді: Q = (p1–p2)pR4/8hL = pR4Dр/8hL = Dр/Х.Гидравликалық кедергі э
шама гидравликалық кедергі деп аталады, сонда Пуазейля формуласы мына түрге келеді: Q = (p1–p2)pR4/8hL = pR4Dр/8hL = Dр/Х.Гидравликалық кедергі э


