Светодиодная лента SNT 60 LED 3528 белая холодная IP65 влагозащищенная 2 страница
Основная статья: Уравнение Дирака (графен)
Рис. 5. Изолинии постоянной энергии (формула (2.4)). Жирный чёрный шестиугольник — перваязона Бриллюэна. Показаны также красные окружности на краях первой зоны Бриллюэна, где закон дисперсии носителей линеен. K и K' обозначают две долины в k -пространстве с неэквивалентными волновыми векторами Из уравнения (2.4) следует, что вблизи точек соприкосновения валентной зоны и зоны проводимости (K и K') закон дисперсии для носителей (электронов) в графене представляется в виде:
где
где Линейный закон дисперсии приводит к линейной зависимости плотности состояний от энергии, в отличие от обычных двумерных систем с параболическим законом дисперсии, где плотность состояний не зависит от энергии. Плотность состояний в графене задаётся стандартным способом
где выражение под интегралом и есть искомая плотность состояний (на единицу площади)[52]:
где Концентрация электронов задаётся интегралом по энергии
где
Концентрацией носителей управляют с помощью затворного напряжения. Они связаны простым соотношением Здесь также следует обратить внимание на тот факт, что появление линейного закона дисперсии при рассмотрении гексагональной решётки не является уникальной особенностью для данного типа кристаллической структуры, а может появляться и при существенном искажении решётки вплоть доквадратной решётки[53][54]. Эффективная масса [править | править вики-текст] Благодаря линейному закону дисперсии эффективная масса электронов и дырок в графене равна нулю. Но в магнитном поле возникает другая масса, связанная с движением электрона по замкнутым орбитам и называемая циклотронной массой. Связь между циклотронной массой и энергетическим спектром для носителей в графене получается из следующего рассмотрения. Энергия уровней Ландау для уравнения Дирака задаётся в виде
где «±» соответствует псевдоспиновому расщеплению[11]. Плотность состояний в графене осциллирует как функция обратного магнитного поля, и её частота равна
где Из периода осцилляций также можно определить концентрацию носителей
Циклотронная масса связана с площадью орбиты следующим соотношением
Если принять во внимание линейный закон дисперсии для носителей в графене (3.1), то зависимость эффективной массы от концентрации задаётся формулой
Согласие этой корневой зависимости с экспериментальными результатами стало доказательством линейности закона дисперсии в графене[11][32]. Хиральность и парадокс Клейна [править | править вики-текст] Основная статья: Парадокс Клейна (графен) Рассмотрим часть гамильтониана для долины K (см. формулу (3.2)):
Матрицы Паули здесь не имеют отношения к спину электрона, а отражают вклад двух подрешёток в формирование двухкомпонентной волновой функции частицы. Матрицы Паули являются операторами псевдоспина по аналогии со спином электрона. Данный гамильтониан полностью эквивалентен гамильтониану для нейтрино, и, как и для нейтрино, существует сохраняющаяся величина проекции спина (псевдоспина для частиц в графене) на направление движения — величина, называемая спиральностью (хиральностью). Для электронов хиральность положительна, а для дырок — отрицательна. Сохранение хиральности в графене приводит к такому явлению, как парадокс Клейна. В квантовой механике с этим явлением связано нетривиальное поведение коэффициента прохождения релятивистской частицей потенциальных барьеров, высота которых больше, чем удвоенная энергия покоя частицы. Частица более легко преодолевает более высокий барьер. Для частиц в графене можно построить аналог парадокса Клейна с той разницей, что не существует массы покоя. Можно показать[55], что электрон преодолевает с вероятностью, равной единице, любые потенциальные барьеры при нормальном падении на границу раздела. Если падение происходит под углом, то существует некоторая вероятность отражения. Например, обычный p-n переход в графене является таким преодолимым барьером[56]. В целом парадокс Клейна приводит к тому, что частицы в графене трудно локализовать, что в свою очередь приводит, например, к высокой подвижности носителей в графене. Недавно были предложены несколько моделей, позволяющих локализовать электроны в графене[57][58]. В работе[59] впервые продемонстрирована квантовая точка из графена и измерена кулоновская блокада при 0,3 К. Эффект Казимира [править | править вики-текст] Эффект Казимира определяет взаимодействие любых электрически нейтральных объектов на малых расстояниях (порядка микрона и меньше). В случае реалистичных материалов величина взаимодействия обуславливается объёмными свойствами материала (диэлектрическая проницаемость в случае диэлектриков, проводимость для металлов). Однако расчёты показывают, что и для моноатомных слоёв графена сила Казимира может быть сравнительно велика, а наблюдение эффекта может быть доступно экспериментально.[60][61] Проводимость [править | править вики-текст] Основные статьи: Проводимость (графен), Подвешенный графен Теоретически показано, что основное ограничение на подвижность электронов и дырок в графене (на Si подложке) возникает из-за заряженных примесей в диэлектрике (SiO2), поэтому сейчас ведутся работы по получению свободновисящих плёнок графена, что должно увеличить подвижность до 2·106 см²·В−1·c−1[62]. В настоящее время максимальная достигнутая подвижность составляет 2·105 см²·В−1·c−1; она была получена в образце, подвешенном над слоем диэлектрика на высоте 150 нм (часть диэлектрика была удалена с помощью жидкостного травителя)[63]. Образец с толщиной в один атом поддерживался при помощи широких контактов. Для улучшения подвижности образец подвергался очистке от примесей на поверхности посредством пропускания тока[64], который нагревал весь образец до 900 К в высоком вакууме. Идеальную двумерную плёнку в свободном состоянии нельзя получить из-за её термодинамической нестабильности. Но если в плёнке будут дефекты или она будет деформирована в пространстве (в третьем измерении), то такая «неидеальная» плёнка может существовать без контакта с подложкой[65]. В эксперименте[66] с использованием просвечивающего электронного микроскопа было показано, что свободные плёнки графена существуют и образуют поверхность сложной волнистой формы, с латеральными размерами пространственных неоднородностей около 5—10 нм и высотой 1 нм. В статье[67]было показано, что можно создать свободную от контакта с подложкой плёнку, закреплённую с двух краёв, образуя, таким образом, наноэлектромеханическую систему. В данном случае подвешенный графен можно рассматривать как мембрану, изменение частоты механических колебаний которой предлагается использовать для детектирования массы, силы и заряда, то есть использовать в качестве высокочувствительного сенсора. Подложка кремния с диэлектриком, на котором покоится[7] графен, должна быть сильно легирована, чтобы её можно было использовать в качествеобратного затвора, при помощи которого можно управлять концентрацией и даже изменять тип проводимости. Поскольку графен является полуметаллом, то приложение положительного напряжения к затвору приводит к электронной проводимости графена, и напротив — если приложить отрицательное напряжение, то основными носителями станут дырки, поэтому в принципе нельзя обеднить полностью графен от носителей. Заметим, что если графит состоит из нескольких десятков слоёв, то электрическое поле достаточно хорошо экранировано, как и в металлах, огромным количеством носителей в полуметалле[30]. В идеальном случае, когда отсутствует легирование и затворное напряжение равно нулю, не должно быть носителей тока (см. плотность состояний), что, если следовать наивным представлениям, должно приводить к отсутствию проводимости. Но, как показывают эксперименты и теоретические работы[68][69][70], вблизи дираковской точки или точки электронейтральности для дираковских фермионов существует конечное значение проводимости, хотя величина минимальной проводимости зависит от метода расчёта. Эта идеальная область не изучена просто потому, что нет достаточно чистых образцов. В действительности все плёнки графена соединены с подложкой, и это приводит к неоднородностям, флуктуациям потенциала, что ведёт к пространственной неоднородности типа проводимости по образцу, поэтому даже в точке электронейтральности концентрация носителей теоретически не меньше, чем 1012 см−2. Здесь проявляется отличие от обычных систем с двумерным электронным или дырочным газом, а именно — отсутствуетпереход металл-диэлектрик. Квантовый эффект Холла [править | править вики-текст] Основная статья: Квантовый эффект Холла (графен)
Рис. 6. a) Квантовый эффект Холла в обычной двумерной системе. b) Квантовый эффект Холла в графене. Впервые аномальный (англ. unconventional) КЭХ или полуцелый квантовый эффект Холла наблюдали в 2005 году в работах[23][32], где было показано, что носители в графене действительно обладают нулевой эффективной массой, поскольку положения плато на зависимости недиагональной компоненты тензора проводимости соответствовали полуцелым значениям холловской проводимости Квантовый эффект Холла (КЭХ) может использоваться как эталон сопротивления, потому что численное значение наблюдаемого в графене плато, равное Двухслойный графен[править | править вики-текст] Основная статья: Двухслойный графен Двухслойный графен — это другая двумерная аллотропная модификация углерода, состоящая из двух слоёв графена. Если B-подрешётка второго слоя расположена над подрешёткой A первого слоя (так называемая упаковка Бернала, аналогичная графиту), то слои расположены на расстоянии около 0,335 нм, благодаря чему электроны из одного слоя графена могут туннелировать в другой. При таком расположении слоёв они повёрнуты на 60 градусов относительно друг друга, и элементарную ячейку можно выбрать как для графена, но с четырьмя атомами в ней. Туннелирование между слоями приводит к гораздо более сложному, отличному от графена, но всё ещё бесщелевому спектру. Транспортные свойства двухслойного графена были впервые исследованы в Манчестерском университете в лаборатории А. Гейма.[72]. Оказалось, что, меняя концентрацию в отдельном слое, можно создать электрическое поле между слоями, которое приводит к формированию запрещённой зоны[73]. Сложность создания запрещённой зоны в графене и относительная свобода для этого в двухслойном графене позволила говорить о том, что графен стал ближе к тому, чтобы сравниться с кремнием в технологии. Интересные факты[править | править вики-текст]
Рис. 7. Для получения нанотрубки (n, m) графитовую плоскость надо разрезать по направлениям пунктирных линий и свернуть вдоль направления вектора R · В статье, опубликованной 10 ноября 2005 года в журнале Nature[11], Константин Новосёлов и Андрей Геймутверждают, что электрические заряды в графене ведут себя как релятивистские частицы с нулевой эффективной массой. Эти частицы, известные как безмассовые фермионы Дирака, описываются уравнением Дирака, хотя вэффекте Шубникова-де Гааза (осцилляции магнетосопротивления) наблюдаемые осцилляции соответствуют конечной циклотронной массе. · Так как закон дисперсии для носителей идентичен закону для безмассовых частиц, графен может выступать в качестве экспериментальной лаборатории для квантовой электродинамики[74]. · Квантовый эффект Холла в графене может наблюдаться даже при комнатной температуре[71] благодаря большой циклотронной энергии, при которой температурное размытие функции распределения Ферми-Дирака меньше этой энергии · При сворачивании графена в цилиндр (см. рис. 7) получается одностенная нанотрубка. В зависимости от конкретной схемы сворачивания графитовой плоскости, нанотрубки могут обладать или металлическими, или полупроводниковыми свойствами[76]. · В графене отсутствует вигнеровская кристаллизация[77]. · В графене нарушается приближение Борна-Оппенгеймера (адиабатическое приближение), гласящее, что в силу медленного движения ионных остовов решётки их можно включить в рассмотрение как возмущение, известное как фононы решётки, — основное приближение, на котором строится зонная теория твёрдых тел[78]. · Термоэлектрический эффект для графена превосходит резистивный омический нагрев, что в перспективе позволит создание на его базе схем, не требующих охлаждения[79][80]. · В двойном слое графена электроны ведут себя как жидкий кристалл[81]. · В медицинских исследованиях графен демонстрирует противораковые свойства. Команда исследователей из Университета Манчестера в Великобритании во главе с Майклом Лизанти (Michael Lisanti) опубликовали статью в журнале Oncotarget, посвященную тому, как окись графена выборочно поражает стволовые клетки, относящиеся к категории раковых. [82] [83] Во время исследования ученые оценили эффекты графена при шести разных видах рака: молочной железы, легких, поджелудочной железы, простаты, яичников и головного мозга. Во всех случаях получен положительный результат. Предполагается, что графен может быть эффективен при широком диапазоне опухолей. См. также[править | править вики-текст]
· Плазменные волны в графене · Графеновый полевой транзистор · Фуллерены · Нанотрубки · Силицен · 2D нанореактор Примечания[править | править вики-текст] ↑ Показывать компактно 1. ↑ Перейти к: 12345 Novoselov et. al., 2004 2. ↑; Katsnelson, 2012, с. 6 3. ↑ Перейти к: 123 Katsnelson, 2012, с. 10—14 4. ↑; Bunch J. S. et. al. Electromechanical Resonators from Graphene Sheets Science 315, 490 (2007) DOI:10.1126/science.1136836 5. ↑; Balandin A. A. cond-mat/0802.1367 6. ↑ Перейти к: 12 Chen Zh. et. al. Graphene Nano-Ribbon Electronics Physica E 40, 228 (2007)DOI:10.1016/j.physe.2007.06.020 7. ↑ Перейти к: 1234 Novoselov K. S. et al. «Electric Field Effect in Atomically Thin Carbon Films», Science 306, 666 (2004) DOI:10.1126/science.1102896 8. ↑ Перейти к: 123 Novoselov, K. S. et al. «Two-dimensional atomic crystals», PNAS 102, 10451 (2005) DOI:10.1073/pnas.0502848102 9. ↑ Перейти к: 12 Rollings E. et. al. Synthesis and characterization of atomically thin graphite films on a silicon carbide substrate J. Phys. Chem. Solids 67, 2172 (2006)DOI:10.1016/j.jpcs.2006.05.010 10. ↑ Перейти к: 12 Hass J. et. al. Highly ordered graphene for two dimensional electronics Applied Physics Letters 89, 143106 (2006) DOI:10.1063/1.2358299 11. ↑ Перейти к: 123456 Novoselov K. S. et al. «Two-dimensional gas of massless Dirac fermions in graphene», Nature 438, 197 (2005) DOI:10.1038/nature04233 12. ↑; Стали известны имена лауреатов Нобелевской премии по физике 13. ↑; The Nobel Prize in Physics 2010 (англ.). NobelPrize.org. Проверено 8 января 2011.Архивировано из первоисточника 24 января 2012. 14. ↑; Премию Спинозы вручили за графен 15. ↑; Cooper, 2012 16. ↑; Lin Y., Valdes-Garcia A., Han S., Farmer D. B., Meric I., Sun Y., Wu Y., Dimitrakopoulos C., Grill A., Avouris P., Jenkins K. A. Wafer-Scale Graphene Integrated Circuit (англ.) // Science. — 2011. — С. 1294—1297. —DOI:10.1126/science.1204428 17. ↑; Yang H., Heo J., Park S., Song H. J., Seo D. H., Byun K., Kim P., Yoo I., Chung H., Kim K. Graphene Barristor, a Triode Device with a Gate-Controlled Schottky Barrier (англ.) // Science. — 2012. — С. 1140—1143. —DOI:10.1126/science.1220527 18. ↑ Перейти к: 12 Schwierz, 2010 19. ↑; Katsnelson, 2012, с. 161—163 20. ↑; Tzalenchuk A., Lara-Avila S., Kalaboukhov A., Paolillo S., Syväjärvi M., Yakimova R., Kazakova O., Janssen T. J. B. M., Fal'ko V., Kubatkin S. Towards a quantum resistance standard based on epitaxial graphene (англ.) // Nature Nanotechnology. — 2010. — С. 186—189. — DOI:10.1038/nnano.2009.474 —arΧiv: 0909.1220 21. ↑; Gusynin, 2007 22. ↑; Katsnelson, 2012 23. ↑ Перейти к: 123 Novoselov et. al. Nature, 2005 24. ↑; Malard, 2009 25. ↑; Bae, 2010 26. ↑ Перейти к: 123 Wallace P. R. «The Band Theory of Graphite», Phys. Rev. 71, 622 (1947)DOI:10.1103/PhysRev.71.622 27. ↑ Перейти к: 123 Shioyama H. Cleavage of graphite to graphene J. Mat. Sci. Lett. 20, 499—500 (2001) 28. ↑; Peierls R., Helv. Phys. Acta 7, 81 (1934); Peierls R., Ann. I. H. Poincare 5, 177 (1935); Landau L. D., Phys. Z. Sowjetvunion 11, 26 (1937) 29. ↑; Ландау Л. Д., Лифшиц Е. М. Статистическая физика. — 2001. 30. ↑ Перейти к: 12 Zhang Y. et al. Fabrication and electric-field-dependent transport measurements of mesoscopic graphite devices Appl. Phys. Lett. 86, 073104 (2005)DOI:10.1063/1.1862334 31. ↑; В Магеллановых облаках нашли следы графена 32. ↑ Перейти к: 123 Zhang Y. et. al. «Experimental observation of the quantum Hall effect and Berry’s phase in graphene» Nature 438, 201 (2005) DOI:10.1038/nature04235 33. ↑; Solution Properties of Graphite and Graphene Sandip Niyogi, Elena Bekyarova, Mikhail E. Itkis, Jared L. McWilliams, Mark A. Hamon, and Robert C. Haddon J. Am. Chem. Soc.; 2006; 128(24) pp 7720 — 7721; (Communication)DOI:10.1021/ja060680r 34. ↑; Bunch J. S. et al. Coulomb Oscillations and Hall Effect in Quasi-2D Graphite Quantum Dots Nano Lett. 5, 287 (2005) DOI:10.1021/nl048111+ 35. ↑; Boehm’s 1961 isolation of graphene. Graphene Times (2009-12-07). Retrieved on 2010-12-10. 36. ↑; Laser Scribing of High-Performance and Flexible Graphene-Based Electrochemical Capacitors. Sciencemag.org (16 марта 2012). Проверено 2 мая 2013. Архивировано из первоисточника 16 июня 2013. 37. ↑; Marcus, Jennifer Researchers develop graphene supercapacitor holding promise for portable electronics / UCLA Newsroom. Newsroom.ucla.edu (15 марта 2012).Проверено 2 мая 2013. Архивировано из первоисточника 16 июня 2013. 38. ↑; Stankovich S. et al. «Stable aqueous dispersions of graphitic nanoplatelets via the reduction of exfoliated graphite oxide in the presence of poly(sodium 4-styrenesulfonate)», J. Mater. Chem. 16, 155 (2006) DOI:10.1039/b512799h 39. ↑; Stankovich S. et al. «Graphene-based composite materials», Nature 442, 282 (2006)DOI:10.1038/nature04969 40. ↑; Wang J. J. et. al. Free-standing subnanometer graphite sheets Appl. Phys. Lett. 85, 1265 (2004) DOI:10.1063/1.1782253 41. ↑; Parvizi F., et. al. Graphene Synthesis via the High Pressure — High Temperature Growth Process Micro Nano Lett., 3, 29 (2008) DOI:10.1049/mnl:20070074Препринт 42. ↑; Sidorov A. N. et al.,Electrostatic deposition of graphene Nanotechnology 18, 135301 (2007) DOI:10.1088/0957-4484/18/13/135301 43. ↑; Berger, C. et al. «Electronic Confinement and Coherence in Patterned Epitaxial Graphene», Science 312, 1191 (2006) DOI:10.1126/science.1125925 44. ↑; J. Hass et. al. Why Multilayer Graphene on 4H-SiC(000-1) Behaves Like a Single Sheet of Graphene Phys. Rev. Lett. 100, 125504 (2008). 45. ↑; Carbon-Based Electronics: Researchers Develop Foundation for Circuitry and Devices Based on Graphite March 14, 2006 gtresearchnews.gatech.edu Link 46. ↑; Schedin F. et. al. Detection of Individual Gas Molecules Absorbed on Graphene Nature Materials 6, 652 (2007) DOI:10.1038/nmat1967 47. ↑; Hwang E. H. et. al. Transport in chemically doped graphene in the presence of adsorbed molecules Phys. Rev. B 76, 195421 (2007)DOI:10.1103/PhysRevB.76.195421
|



 — скорость Ферми (экспериментальное значение[11]
— скорость Ферми (экспериментальное значение[11]  — модуль волнового вектора в двумерном пространстве с компонентами
— модуль волнового вектора в двумерном пространстве с компонентами 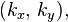 отсчитанного от K или K' точек Дирака,
отсчитанного от K или K' точек Дирака,  — постоянная Планка. Здесь следует отметить, что такого рода спектром обладает фотон, поэтому говорят, что квазичастицы (электроны и дырки, энергия для которых выражается формулой
— постоянная Планка. Здесь следует отметить, что такого рода спектром обладает фотон, поэтому говорят, что квазичастицы (электроны и дырки, энергия для которых выражается формулой  ) в графене обладают нулевой эффективной массой. Скорость Ферми
) в графене обладают нулевой эффективной массой. Скорость Ферми 
 — вектор-строка, состоящий из матриц Паули.
— вектор-строка, состоящий из матриц Паули.

 и
и  — спиновое и долинное вырождение соответственно, а модуль энергии появляется, чтобы описать электроны и дырки одной формулой. Отсюда видно, что при нулевой энергии плотность состояний равна нулю, то есть отсутствуют носители (при нулевой температуре).
— спиновое и долинное вырождение соответственно, а модуль энергии появляется, чтобы описать электроны и дырки одной формулой. Отсюда видно, что при нулевой энергии плотность состояний равна нулю, то есть отсутствуют носители (при нулевой температуре).
 — уровень Ферми. Если температура мала по сравнению с уровнем Ферми, то можно ограничиться случаем вырожденного электронного газа
— уровень Ферми. Если температура мала по сравнению с уровнем Ферми, то можно ограничиться случаем вырожденного электронного газа
 при толщине диэлектрика 300 нм. При такой толщине эффектами квантовой ёмкости можно принебречь, хотя при уменьшении расстояния до затвора в десять раз концентрация уже не будет линейной функцией приложенного напряжения.
при толщине диэлектрика 300 нм. При такой толщине эффектами квантовой ёмкости можно принебречь, хотя при уменьшении расстояния до затвора в десять раз концентрация уже не будет линейной функцией приложенного напряжения.

 — площадь орбиты в пространстве волновых векторов на уровне Ферми. Осциллирующий характер плотности состояний приводит к осцилляциям магнетосопротивления, что эквивалентно эффекту Шубникова — де Гааза в обычных двумерных системах. Исследуя температурную зависимость амплитуды осцилляций, находят циклотронную массу носителей.
— площадь орбиты в пространстве волновых векторов на уровне Ферми. Осциллирующий характер плотности состояний приводит к осцилляциям магнетосопротивления, что эквивалентно эффекту Шубникова — де Гааза в обычных двумерных системах. Исследуя температурную зависимость амплитуды осцилляций, находят циклотронную массу носителей.




 — вырождение спектра
— вырождение спектра в единицах
в единицах  (множитель 4 появляется из-за четырёхкратного вырождения энергии), то есть
(множитель 4 появляется из-за четырёхкратного вырождения энергии), то есть 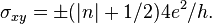 Это квантование согласуется с теорией квантового эффекта Холла для дираковских фермионов[70][69]. Сравнение целочисленного квантового эффекта Холла в обычной двумерной системе и графене см. на рисунке 6. Здесь показаны уширенные уровни Ландау для электронов (выделение красным цветом) и для дырок (синий цвет). Если уровень Ферми находится между уровнями Ландау, то на зависимости холловской проводимости
Это квантование согласуется с теорией квантового эффекта Холла для дираковских фермионов[70][69]. Сравнение целочисленного квантового эффекта Холла в обычной двумерной системе и графене см. на рисунке 6. Здесь показаны уширенные уровни Ландау для электронов (выделение красным цветом) и для дырок (синий цвет). Если уровень Ферми находится между уровнями Ландау, то на зависимости холловской проводимости  наблюдается ряд плато. Эта зависимость отличается от обычных двумерных систем (аналогом может служить двумерный электронный газ в кремнии, который является двухдолинным полупроводником в плоскостях, эквивалентных {100}, то есть тоже обладает дополнительным четырёхкратным вырождением уровней, и холловские плато наблюдаются при
наблюдается ряд плато. Эта зависимость отличается от обычных двумерных систем (аналогом может служить двумерный электронный газ в кремнии, который является двухдолинным полупроводником в плоскостях, эквивалентных {100}, то есть тоже обладает дополнительным четырёхкратным вырождением уровней, и холловские плато наблюдаются при 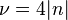 ).
). воспроизводится с хорошей точностью, хотя качество образцов уступает высокоподвижному ДЭГ в GaAs и, соответственно, точности квантования. Преимущество КЭХ в графене в том, что он наблюдается при комнатной температуре[71] (в магнитных полях свыше 20 Т). Основное ограничение на наблюдение КЭХ при комнатной температуре накладывает не размытие распределения Ферми — Дирака, а рассеяние носителей на дефектах, что приводит к уширению уровней Ландау.
воспроизводится с хорошей точностью, хотя качество образцов уступает высокоподвижному ДЭГ в GaAs и, соответственно, точности квантования. Преимущество КЭХ в графене в том, что он наблюдается при комнатной температуре[71] (в магнитных полях свыше 20 Т). Основное ограничение на наблюдение КЭХ при комнатной температуре накладывает не размытие распределения Ферми — Дирака, а рассеяние носителей на дефектах, что приводит к уширению уровней Ландау.
 (это расстояние между первым и нулевым уровнями Ландау равно 1200 K при магнитном поле 9 Т)[75].
(это расстояние между первым и нулевым уровнями Ландау равно 1200 K при магнитном поле 9 Т)[75].




