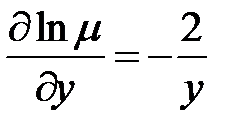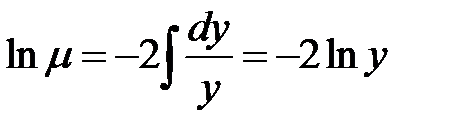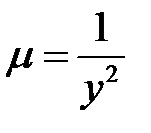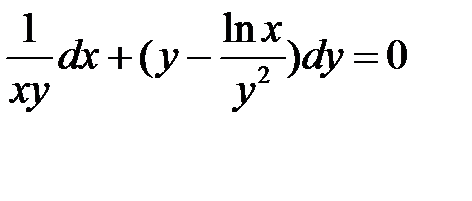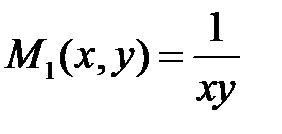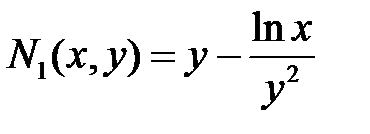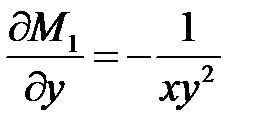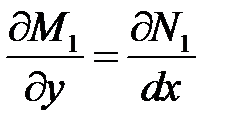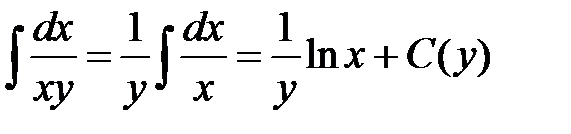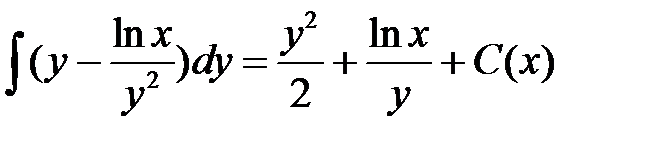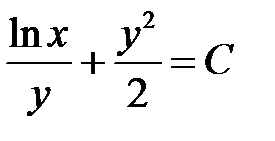Интегрирующий множительПусть для уравнения не выполняется условие Иногда удается подобрать такую функцию Найдем формулы, по которым можно вычислить интегрирующий множитель. Умножим обе части уравнения (1) на множитель
Для того, чтобы это уравнение было уравнением в полных дифференциалах, необходимо и достаточно выполнение условия
т.е. или Разделим обе части этого равенства на
Всякая функция Уравнение (2) является уравнением в частных производных с неизвестной функцией Задача нахождения Пусть Из уравнения (2) получаем обыкновенное дифференциальное уравнение Его можно решить, если только выражение Аналогично, если Из уравнения (2) получим уравнение
Решаем его, если выражение Пример. Г.Н. Берман № 4061
Выражение Выражение
Умножим обе части данного уравнения на
Новое уравнение есть уравнение в полных дифференциалах.
Общее решение данного уравнения
|
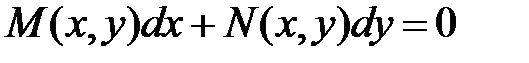(1)
, т.е. 
.
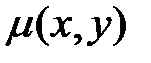, после умножения на которую всех членов уравнения (1), левая часть уравнения становится полным дифференциалом. Общее решение полученного уравнения совпадает с общим решением первоначального уравнения. Функция 
:
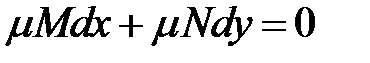
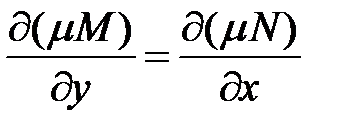
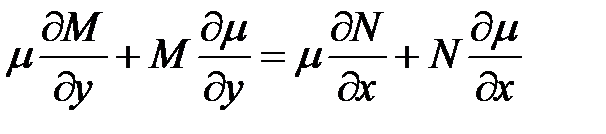
(2)
- интегрирующий множитель, который зависит только от у, тогда 
.
, из которого определим 
, а затем 
зависит только от у.
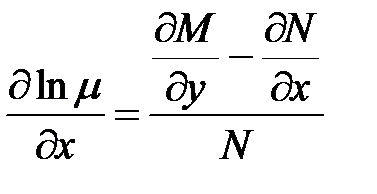
- интегрирующий множитель, зависит только от х.
зависит только от х.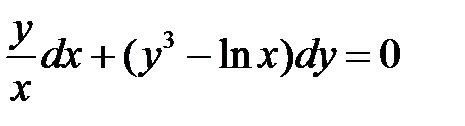
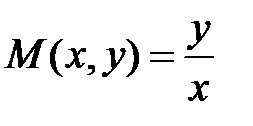
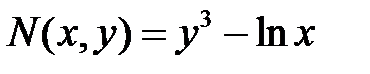
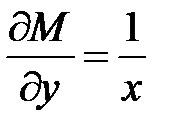
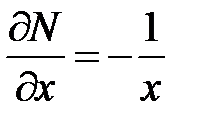
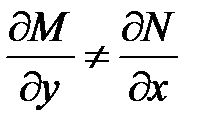
не подходит
подходит
