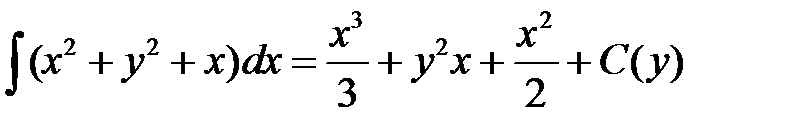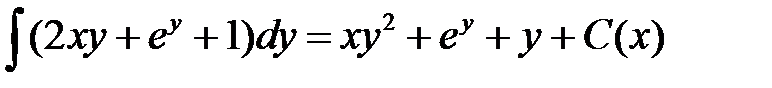Уравнение в полных дифференциалах.
Определение. Уравнение
называется уравнением в полных дифференциалах, если
причем При выполнении условия (2) левая часть уравнения (1) представляет полный дифференциал некоторой функции Уравнение (1) можно записать в виде
Общее решение этого уравнения будет
где С – произвольная постоянная. Полный дифференциал некоторой функции
т.е. Тогда Дифференцируя 1 ое соотношение по у, а 2 ое по х получим
Т.к. т.е. равенство (2) является необходимым условием для того, чтобы левая часть уравнения (1) была полным дифференциалом некоторой функции Из соотношения При интегрировании по х, у – считали постоянной, поэтому она входит в состав произвольной постоянной. Подберем функцию
Учитывая, что
Итак,
Точка Общее решение уравнения (1) запишем так:
Пример.
Условие
Общее решение
|

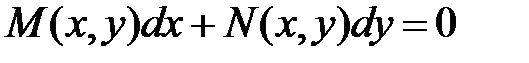 (1)
(1)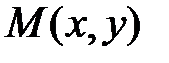 и
и 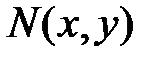 - непрерывные, дифференцируемые функции, для которых выполняется соотношение
- непрерывные, дифференцируемые функции, для которых выполняется соотношение , (2)
, (2)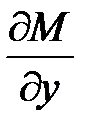 и
и  непрерывны в некоторой области.
непрерывны в некоторой области.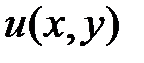 .
.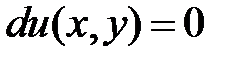 (3)
(3)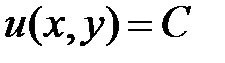 ,
, выражается формулой
выражается формулой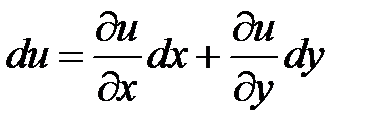 ,
,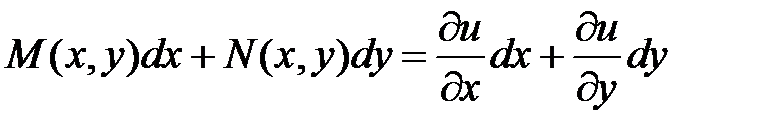 .
.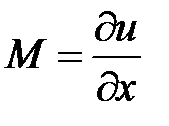 ,
,  (4)
(4)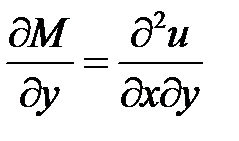 ,
,  .
.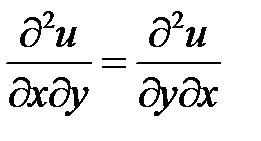 , то
, то  ,
,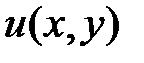 . Покажем, что это условие является и достаточным, т.е. при выполнении условия (2) левая часть уравнения (1) есть полный дифференциал некоторой функции
. Покажем, что это условие является и достаточным, т.е. при выполнении условия (2) левая часть уравнения (1) есть полный дифференциал некоторой функции 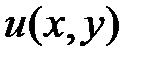 .
. находим
находим 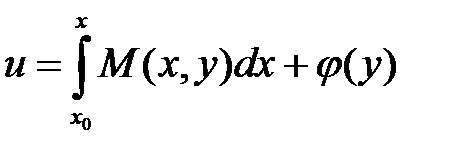 , где
, где  - область решения.
- область решения.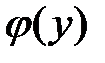 так, чтобы выполнялось второе условие равенства (4). Продифференцируем последнее равенство по у
так, чтобы выполнялось второе условие равенства (4). Продифференцируем последнее равенство по у
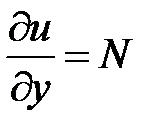 ,
, 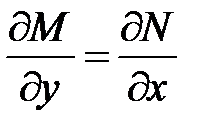 , можем написать
, можем написать 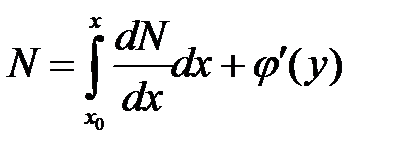
 или
или 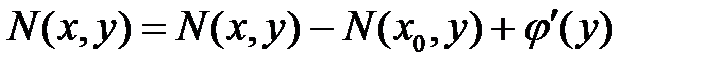 , откуда
, откуда 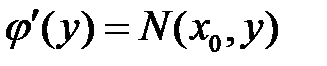 или
или 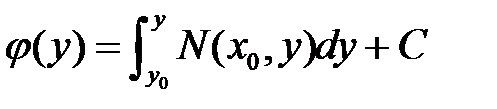 .
.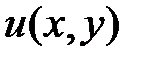 будет иметь вид
будет иметь вид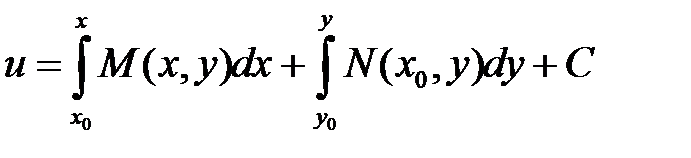
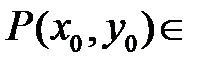 области, в которой существует решение уравнения (1).
области, в которой существует решение уравнения (1).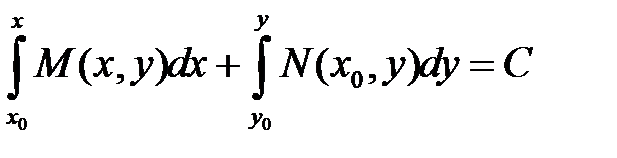
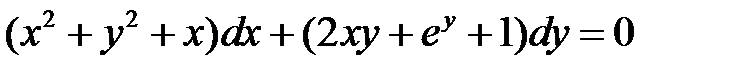
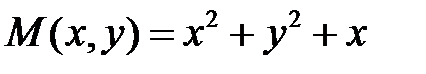
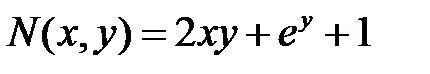


 выполняется
выполняется