Капиллярные явления
В зависимости от соотношения энергий адгезии и когезии (межмолекулярного взаимодействия внутри объема самого вещества), на поверхности раздела фаз действуют силы поверхностного натяжения. Поэтому капля жидкости, лежащей на твердой поверхности, получает определенную форму (рис.2)
cos θ; = (γ; 13 −; γ; 12)/ γ; 23 (3) здесь θ; − краевой угол ( угол смачивания). θ острый в случае смачивания и тупой при несмачивании. При контакте жидкости с твердым телом поверхность жидкости искривляется и становится либо выпуклой либо вогнутой. Силы поверхностного натяжения дают равнодействующую, направленную всегда в сторону центра кривизны. Таким образом, внутри всякой искривленной поверхности создается добавочное, вызванное именно кривизной поверхности, давление. Капиллярные явления Следствием этого являются капиллярные явления. Если поместить узкую трубку (капилляр) одним концом в жидкость, налитую в широкий сосуд, то вследствие смачивания или несмачивания жидкостью стенок капилляра кривизна мениска − поверхности жидкости в капилляре становится значительной. В случае смачивания мениск вогнутый, при несмачивании − выпуклый. Над вогнутой поверхностью воды создается дефицит давления Δ Р. Вследствие этого жидкость поднимается по капилляру на такую высоту h, чтобы вес столбика жидкости на уровнем воды в сосуде уравнял бы силу давления этого дефицита: Vρg = πr2hρg = πr2 Δ Р =2 πrγ; где V – объем жидкости; ρ −;плотность жидкости g; r − радиус капилляра; πr2 -- площадь сечения и 2πr − окружность сечения капилляра, h – высота столбика жидкости. Имеем тогда высоту столбика воды в капилляре Вода может подниматься по узким капиллярам на значительную высоту (до 3 м), что имеет важное значение в природе. Ступенчатой капиллярной подачей растения обеспечивают живительной влагой листья на кроне на высоту десятки метров. В технике и быту капиллярные явления используются в фитилях, системах смазки, химическом производстве и т.д. Как следует из уравнения (1) поверхностное натяжение в жидкостях помимо энтропийной составляющей имеет адгезионную. Поверхностно-активные вещества (ПАВ) значительно снижают адгезию, тем самым и поверхностное натяжение (например мыло снижает γ; с 0,075 до 0,045 Н/м). Сахар и соль, наоборот, увеличивают γ воды. Поверхностные явления играют важную роль в процессах в живой и неживой природы, во всех областях человеческой жизнедеятельности. В последние годы быстро развиваются нанотехнологии, в которых для получения новых материалов и конструкций реализуются специфические свойства поверхностных слоев.
Описание прибора:
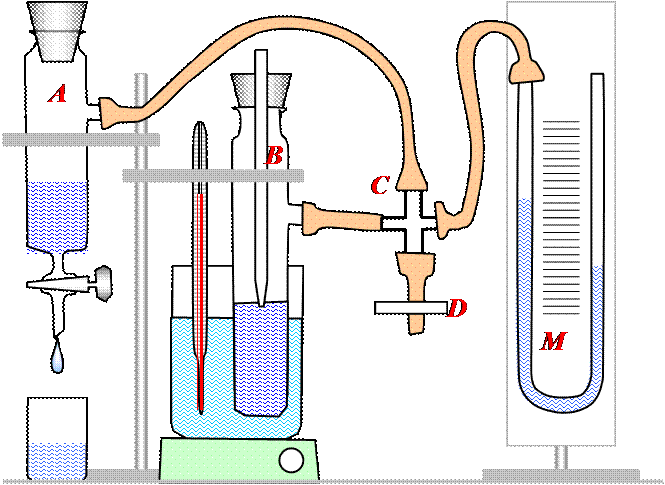
Прибор (см. рис.3) состоит из наполненного водой аспиратора А, соединенного с помощью резиновых трубок четырехконечной трубки С с манометром М и с воздушным верхним пространством плотно закрытого сосуда В, в который наливают некоторое количество исследуемой жидкости. Через отверстие в пробке в этот сосуд вводится так называемый «кончик», представляющий собой стеклянную трубку, нижний конец которой оттянут так, что выход канала весьма узок. Этот «кончик» помещается на уровне испытываемой жидкости, так чтобы он соприкасался с ее поверхностью. Сосуд В помещается для поддержания и изменения температуры в стакан, наполненный водой, который может подогреваться. Четвертый отросток четырехконечной трубки c краном D соединяет всю систему с атмосферой.
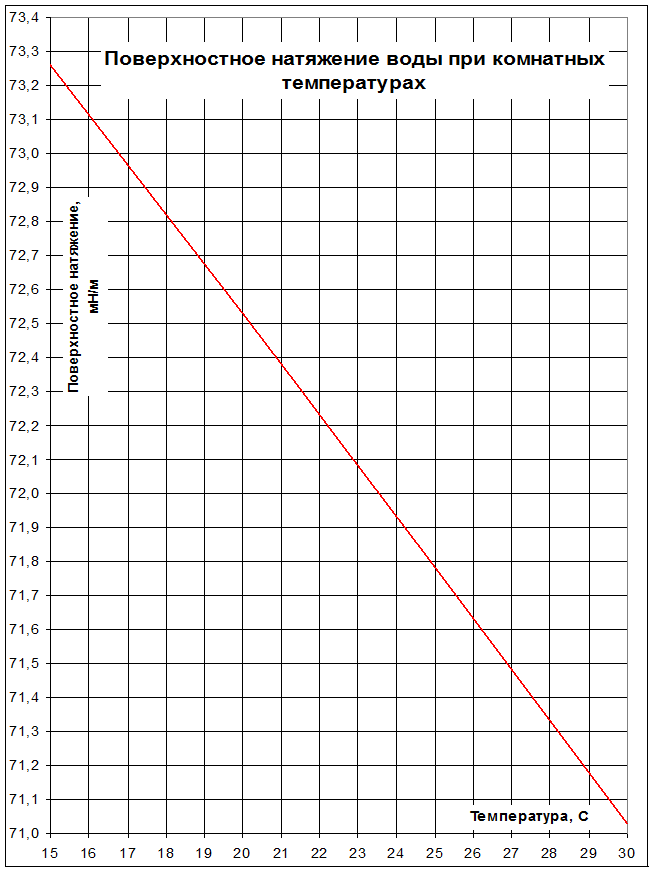
Обозначим эту разность давлений через H, а коэффициент поверхностного натяжения исследуемой жидкости через γ;.Тогда в момент отрыва пузырька между ними будет существовать следующее соотношение: γ = А Н, (4) где А – коэффициент пропорциональности, зависящей от размеров «кончика»; т.е. величина постоянная для данного прибора. Для определения ее необходимо произвести опыт с какой-либо жидкостью, поверхностное натяжение которой хорошо известно, например, с водой (при t= 20ºC у воды γ0 = 0,07253 Н/м, при других значениях комнатной температуры см. приложение 1 ). Тогда, подставив найденное экспериментально значение Н0 и определенное по графику γ0 в формулу (1), будем иметь:
Определяя таким образом постоянную прибора, можно перейти к определению поверхностного натяжения любой жидкости, которая выразится формулой:
Указания по выполнению работы:
А. Определение постоянной прибора.
1. Собрав сосуд по рисунку, налить в аспиратор воды до указанного уровня, указанного на рисунке. 2. Открыть отросток D соединительной стеклянной трубки, устанавливая этим внутри прибора атмосферное давление. Уровни жидкости в коленах манометра при этом выравниваются. 3. Передвигая шкалу манометра, устанавливают нулевое деление ее на общий уровень спирта в коленах. 4. Закрыть отросток D. 5. Открыть кран аспиратора, начнется выделение пузырьков. 6. Отрегулировать кран, чтобы изменение давления происходило достаточно медленно, и можно было легко отсчитать высоты уровней в манометре в момент отрыва пузырька. 7. Когда частота образования пузырьков установится, начать производить отсчет Н0 по манометру, отмечая высоту уровня в обоих коленах. 8. Отсчет производится не менее чем для 10 пузырьков, по ним вычисляется среднее значение Н0. 9. Одновременно определить температуру в стакане с водой, в который погружен сосуд В. 10. Подставив в формулу (3) полученное значение Н0 и взятое из таблиц или графиков значение γ0 для данной температуры, находят постоянную прибора. Б.Определение зависимости γ от концентрации растворов.
1. Наполнить сосуд В раствором бутилового спирта в воде определенной концентрации, причем во избежание ошибки рекомендуется предварительно прополоскать сосуд и особенно «кончик» этого прибора. 2. Определить разность давлений при отрыве пузырька (высоту Н) 3. Вычислить значение γ; 4. Повторить измерения для нескольких растворов. 5. Построить график зависимости γ; от концентрации.
В. Определение зависимости γ от температуры. 1. Прополоскать и наполнить сосуд В исследуемой жидкостью. 2. Нагреть воду в стакане, в которой погружен сосуд до 80-90˚ С. 3. Дать воде медленно остыть, производя через каждые 10˚ С отсчет Н. 4. Определить α для температур 80°, 70°, 60°, 50°, 40°, 30°. 5. Построить график зависимости γ; от температуры.
Контрольные вопросы:
1. Поверхность, особенности структуры и свойств 2. Поверхностные явления 3. Поверхностная энергия 4. Поверхностное натяжение 5. Единицы измерения поверхностного натяжения 6. Смачивание и несмачивание 7. Капиллярные явления 8. От чего зависит коэффициент поверхностного натяжения? 9. Что такое поверхностно-активные вещества? 10. Значение поверхностных явлений
Литература 1. Фриш С.З., Тимофеева А.В. Курс общей физики. Т.11 2. Савельев И.В. Курс общей физики. М., Наука, 1977г.
Приложение 1
|

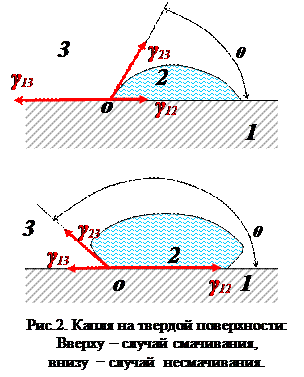 Условие равновесия в точке О между силами поверхностного натяжения γ; 12 −на поверхности раздела «1 (твердое тело) −2 (жидкость)», γ; 13 −на «1−3 (воздух); γ; 23 − на поверхности раздела «2-3»:
Условие равновесия в точке О между силами поверхностного натяжения γ; 12 −на поверхности раздела «1 (твердое тело) −2 (жидкость)», γ; 13 −на «1−3 (воздух); γ; 23 − на поверхности раздела «2-3»: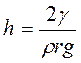 .
.
 (5)
(5) (6)
(6)