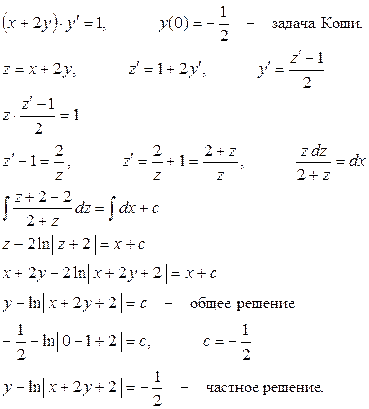Дифференциальные уравнения с разделяющимися переменными.
y ¢ = f(x) ×g (y) или M 1 (x) × N 1 (y)dx + M 2 (x) × N 2 (y)dy = 0 ЗАМЕЧАНИЕ: Пример:
Уравнения, приводимые к уравнениям с разделяющимися переменными. y ¢ = f(a × x + b × y), Замена: z = a × x + b × y Пример:
Пример:
Однородные уравнения первого порядка. ОПРЕДЕЛЕНИЕ: Функция f(x; y) называется однородной функцией n -го измерения, если для любого l выполняется равенство
Пример:
Пример:
Утверждение 1: Если f(x; y) – однородная функция нулевого измерения, то она является функцией аргумента Доказательство:
Утверждение 2: Если функция M(x; y) и функция N(x; y) однородные функции одного измерения, то их отношение есть однородная функция нулевого измерения.
Доказательство:
ОПРЕДЕЛЕНИЕ: Уравнение y ¢ = f(x; y), где f(x; y) – однородная функция нулевого измерения, называется однородным уравнением первого порядка. Проверка однородности:
Решение однородных уравнений первого порядка.
Пример:
Пример:
Уравнения, приводимые к однородным.
УТВЕРЖДЕНИЕ: Если c = c 1 = 0, то (*) – однородное уравнение первого порядка.
Пример:
Пример:
|
. Необходимо привести уравнение к уравнению с разделяющимися переменными, т.е. преобразовать его таким образом, чтобы множитель при dx содержал только переменную x, а множитель при dy – только y. Это действие называется разделением переменных.
