РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В ГРУНТОВОМ МАССИВЕ.

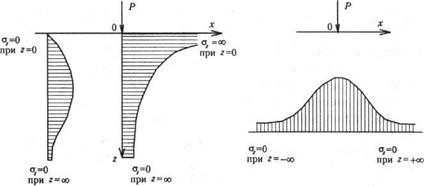
45. Как вычислить вертикальные напряжения в массиве грунта от его собственного веса и чему они равны?

Вертикальное напряжение от собственного веса грунта σ_z представляет собой вес столба грунта над рассматриваемой точкой с площадью поперечного сечения, равной единице. Таким образом, если в точке на глубине z грунт однородный по всей глубине, получаем:

σ_z= γ;z,

Если имеются различные слои, то:

.

Удельный вес грунта ниже горизонта воды принимается с учетом действия выталкивающей силы за счет взвешивания в воде.

На границе водоупора в эпюре σ_z имеет место скачок на величину Δσ _h = γ; _w ·h₂.

 

46. Следует ли учитывать деформации грунта от его собственного веса?

Деформации грунта от его собственного веса обычно не учитываются, так как они давно завершились. Однако в том случае, если в силу обстоятельств изменяется структура грунта, то сила собственного веса грунта вызывает в нем дополнительные деформации (например, при увлажнении лессового грунта, из-за которого растворяются жесткие цементационные связи, или оттаиваний вечномерзлого грунта).

 

47. Какие основные положения приняты в теории упругости?

Основные положения теории упругости следующие:

1. Тело является сплошным и изотропным (деформационные свойства в различных направлениях одинаковы).

2. Тело является упругим и со снятием нагрузки все деформации исчезают.

3. Напряжения в теле отсутствуют, если нет внешней нагрузки.

4. Тело является "бесконечно" прочным, то есть в нем не возникает разрушений и трещин, изменяющих напряженное состояние.

5. Связь между напряжениями и деформациями является линейной и описывается законом Гука.

 

48. Какие основные положения приняты в теории линейно-деформируемых тел?

Для того, чтобы можно было воспользоваться решениями задач, имеющимися в теории упругости, приняты следующие положения:

1. Грунт состоит обычно из трех компонентов: минерального скелета, воды и воздуха, однако возможно его рассматривать как квазисплошное тело, то есть тело, имеющее свойства сплошного однородного тела, в котором трещины и пустоты отсутствуют. Грунт можно рассматривать как тело изотропное, обладающее одинаковыми деформационными свойствами в разных направлениях.

2. Для грунта характерно наличие остаточных деформаций. При полном снятии нагрузки все деформации не исчезают, а упругие (то есть восстанавливающиеся) бывают часто значительно меньше неупругих (остаточных) деформаций. Поэтому в теории линейно-деформируемых тел рассматривается только процесс нагрузки, а процесс разгрузки, если в том есть необходимость, рассматривается особо.

3. Считается, что нагрузки на грунт не вызывают его разрушения и далеки от предельных, поэтому в грунтовом массиве не возникает трещин, разрывов, срезов и т.д., то есть не нарушается "квазисплошность".

4. Связь между полными напряжениями и общими деформациями принимается линейной. Таким образом, считается справедливым закон Гука, связывающий напряжения и деформации. Деформации считаются малыми.

 

49. Чем теория линейно-деформируемых тел отличается от теории упругости?

В теории упругости рассматриваются только упругие тела с восстанавливающимися дефор-мациями, а в теории линейно-деформируемых тел рассматриваются общие деформации, включаю-

щие также остаточную деформацию.

 

50. Решение какой задачи теории упругости для полупространства является основным? Чем обусловлена возможность использования её для решения других практически важных задач?

 

Основным является решение задачи о сосредоточенной силе, приложенной к поверх-ности полупространства перпендикулярно к граничной плоскости (задача Буссинеска). Для решения задач о нагрузке, имеющей горизонтальную составляющую, рассматрива-ется дальнейшее развитие решения этой же задачи, но при сосредоточенной силе, действующей вдоль граничной плоскости (как бы "прикрепленной" к ней в одной точке). Аналогичные решения задач о сосредоточенных силах вертикальной и горизонтальной, то есть приложенных перпендикулярно (решение Фламана) и по касательной к границе полуплоскости, также являются основными. Из них путем, интегрирования могут быть получены многие решения интересующих нас в практических целях задач.

 

51. Действие сосредоточенной силы (основная задача) Какое предположение делается в отношении зоны, расположенной непосредственно у сосредоточенной силы?

Поставленная задача для упругого (а следовательно, и любого линейно деформи-рованного) полупространства впервые была полностью решена проф. Ж.. Буссинеском

(1885), а определение напряжений для площадок, параллельных ограничивающей полупространство плоскости,-проф.В.Кирпичевым и проф.Н.А. Цытовичем (1923-1934).

Задача определить напряжения σ_z, τ_zy,τ_zx, как наиболее часто используемых в расчетах.

 

Для упрощения расчетов определяют напряжения σ_R в точке М с полярными координатами R и β;. Окончательный результат, который полностью совпадает с решением Буссинеска, принимают как постулат, что напряжение σ_R пропорционально cosβ и обратно пропорционально квадрату расстояния от точки приложения сосредоточенной силы R².

Предполагается, что сплошная среда является бесконечно прочной и не может разрушаться. Ж.Буссинеск, чтобы обойти это обстоятельство, не рассматривал небольшую зону, непосредственно находящуюся у сосредоточенной силы.

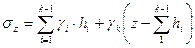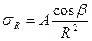Таким образом: ; для перемещений: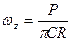

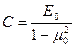где: - коэф.линейно деформируемого полупространства; Е₀ ,μ₀ -модули общей и поперечной (аналогичный коэф. Пуассона) деформаций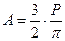

А - некоторый коэффициент, определяемый из условия равновесия:

Подставляя А в формулу получим: .