А4(3,6) - - идентификатор выходного вещественного трехмерного массива, элементами которого являются следующие параметры группы
А4(3,6) = Р(4) - идентификатор входного вещественного массива, элементами которого являются управляющие переменные Р(4) = (Р1, Р2, Р3, Р4); К – идентификатор входной целой переменной, соответствующий коэффициенту сборки к группы. Если все элементы массива Р(4) больше нуля, то вычисляются все кинематические параметры группы. Если Р(1) < 0 – отсутствует точка D. Если Р(2) < 0 – отсутствует точка Е. Если Р(3) < 0 – вычисляются только координаты точек D, E, C и углы a, b и g. Если Р(4) < 0 – вычисляются координаты точек D, E, C и углы a, b и g, а также скоростные параметры группы.
4 МЕТОДИКА СОСТАВЛЕНИЯ АЛГОРИТМА И ПРОГРАММЫ КИНЕМАТИЧЕСКОГО АНАЛИЗА ДВУХПОВОДКВОЙ ГРУППЫ С ВНЕШНЕЙ ПОСТУПАТЕЛЬНОЙ ПАРОЙ
При кинематическом анализе рассматриваемой структурной группы должны быть заданы следующие параметры в соответствии с рисунком 4: координаты, проекции векторов скоростей и ускорений кинематической пары А, которой группа присоединяется к механизму:
координаты, проекции векторов скоростей и ускорений точки Е, принадлежащей направляющей ползуна:
угловые характеристики направляющей ползуна:
линейные и угловые размеры звеньев группы: l, d и g; координаты произвольной точки С в системе подвижных координат коэффициент k. Коэффициент k определяет координаты кинематической пары В относительно кинематической пары А и принимает значения В результате расчета определяются: координаты, проекции векторов скоростей и ускорений кинематической пары
угловые параметры группы:
Вычисление кинематических характеристик группы осуществляется по алгоритму 3. В алгоритме предусмотрена проверка существования сборки звеньев группы - формула 3, которая необходима, например, в алгоритмах синтеза механизмов, для выявления ошибок ввода. Если группа не собирается, т.е. нет точки В, то значению a присваивается большое отрицательное значение, которое выводится на печать. В алгоритме предусмотрена проверка выполнения различных требований: наличие произвольной точки Алгоритм 3 оформлен в виде подпрограммы с именем КАГ2 и составлена инструкция по ее применению.
Алгоритм 3 - Кинематический анализ двухповодковой группы с внешней поступательной парой 1. 2. 3. Если 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Если 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. Если 25. 26. 27. M2: если 28. 29. 30. 31. 32. 33. 34. Если 35. 36. 37. Переход на метку M 3; 38. М 4: 39. M 3: конец алгоритма.
Рисунок 4 – Расчетная схема двухповодковой группы с внешней поступательной парой.
Инструкция к подпрограмме кинематического КАГ2 анализа двухповодковой группы с внешней поступательной парой
ПОДПРОГРАММА КАГ2 (А1, А2, А3, А4, Р, К), где А1(8) – идентификатор входного вещественного массива, элементами которого являются следующие параметры группы А1(8) = (
|

 ;
; ;
; ;
; ;
; , связанных со звеном АВ;
, связанных со звеном АВ; . Коэффициент k принимает значение +1, если при обходе на рисунке 4 контура, образованного точками А, F, D и В, против движения часовой стрелки последовательно встречаются вершины А, F, D и В или А,F,B и D, в противном случае – k = -1. Точка F – точка пересечения перпендикуляра, опущенного из точки А, и направляющей ползуна.
. Коэффициент k принимает значение +1, если при обходе на рисунке 4 контура, образованного точками А, F, D и В, против движения часовой стрелки последовательно встречаются вершины А, F, D и В или А,F,B и D, в противном случае – k = -1. Точка F – точка пересечения перпендикуляра, опущенного из точки А, и направляющей ползуна. , точек
, точек  и
и  :
: ;
;  ;
;  ;
;
 ;
; ;
; то на М 4;
то на М 4;
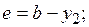

 ;
; ;
; ;
; ;
; ;
; ;
; , то переход на метку
, то переход на метку  ;
; ;
;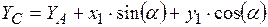 ;
; , то переход на метку M 3;
, то переход на метку M 3; ;
; ;
;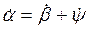 ;
; ;
; ;
; ;
; ;
; ;
; ;
; , то переход на метку M3;
, то переход на метку M3;
 ;
; ;
; ;
;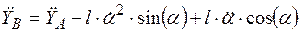 ;
; ;
; ;
; ;
; ;
; и вывод на печать: сборки не существует;
и вывод на печать: сборки не существует;
 );
);


