Первообразная, основное свойство первообразных
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определение. Первообразной функции Поскольку Теорема. Любые две первообразные функции
Доказательство: Обозначим
Определение. Множество всех первообразных одной функции называется неопределенным интегралом этой функции и обозначается Очевидно, что если Приведем таблицу неопределенных интегралов с проверкой того, что действительно производная от правой части совпадает с подынтегральной функцией. Таблица неопределенных интегралов
Приемы интегрирования
Тождественные преобразования подынтегрального выражения и использование свойств интегралов (непосредственное интегрирование).
Из свойства производной
следует аналогичное свойство для неопределенных интегралов
Пример 1.
Пример 2.
|
называется функция 
, производная которой равна 
, т.е. 
.
, где 
постоянная, первообразных функции 
, то
Согласно предположению 
Следовательно, 
имеем:
.
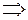
, причем 
называется подынтегральной функцией, 
подынтегральным выражением.
, то 
, где 
.
.
.
.
.
.
.
.
.
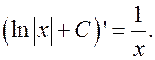
