Нормальные системы линейных однородных дифференциальных
Нормальные системы линейных однородных дифференциальных уравнений с постоянными коэффициентами.
При рассмотрении систем дифференциальных уравнений ограничимся случаем системы трех уравнений (n = 3). Все нижесказанное справедливо для систем произвольного порядка. Определение. Нормальная система дифференциальных уравнений c постоянными коэффициентами называется линейной однородной, если ее можно записать в виде:
Решения системы ищутся в виде: Подставляя эти значения в систему (2) и перенеся все члены в одну сторону и сократив на ekx, получаем:
Для того, чтобы полученная система имела ненулевое решение необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.:
В результате вычисления определителя получаем уравнение третьей степени относительно k. Это уравнение называется характеристическим уравнением и имеет три корня k1, k2, k3. Каждому из этих корней соответствует ненулевое решение системы (2):
Линейная комбинация этих решений с произвольными коэффициентами будет решением системы (2):
Пример. Найти общее решение системы уравнений:
Составим характеристическое уравнение:
Решим систему уравнений:
Для k1: Полагая
Для k2:
Общее решение системы:
Этот пример может быть решен другим способом: Продифференцируем первое уравнение: Подставим в это выражение производную у¢ = 2 x + 2 y из второго уравнения.
Подставим сюда у, выраженное из первого уравнения:
Ряды. Основные определения. Определение. Сумма членов бесконечной числовой последовательности При этом числа Определение. Суммы Таким образом, возможно рассматривать последовательности частичных сумм ряда S1, S2, …,Sn, … Определение. Ряд
Определение. Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся и ему не ставят в соответствие никакой суммы.
Свойства рядов. 1) Сходимость или расходимость ряда не нарушится если изменить, отбросить или добавить конечное число членов ряда. 2) Рассмотрим два ряда Теорема. Если ряд 3) Рассмотрим два ряда Теорема. Если ряды
Разность двух сходящихся рядов также будет сходящимся рядом. Сумма сходящегося и расходящегося рядов будет расходящимся рядом. О сумме двух расходящихся рядов общего утверждения сделать нельзя. При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.
Критерий Коши. (необходимые и достаточные условия сходимости ряда)
Для того, чтобы последовательность
Сформулируем критерий Коши для ряда. Для того, чтобы ряд
Однако, на практике использовать непосредственно критерий Коши не очень удобно. Поэтому как правило используются более простые признаки сходимости: 1) Если ряд Пример. Исследовать сходимость ряда Найдем 2) Если ряд сходится, то последовательность его частных сумм ограничена. Однако, этот признак также не является достаточным. Например, ряд 1-1+1-1+1-1+ … +(-1)n+1+… расходится, т.к. расходится последовательность его частных сумм в силу того, что
Однако, при этом последовательность частных сумм ограничена, т.к.
Ряды с неотрицательными членами. При изучении знакопостоянных рядов ограничимся рассмотрением рядов с неотрицательными членами, т.к. при простом умножении на –1 из этих рядов можно получить ряды с отрицательными членами. Теорема. Для сходимости ряда Признак сравнения рядов с неотрицательными членами. Пусть даны два ряда
Теорема. Если un £ vn при любом n, то из сходимости ряда Пример. Исследовать на сходимость ряд Т.к. Пример. Исследовать на сходимость ряд Т.к. Также используется следующий признак сходимости: Теорема. Если Признак Даламбера. (Жан Лерон Даламбер (1717 – 1783) – французский математик) Если для ряда
Предельный признак Даламбера.
Предельный признак Даламбера является следствием из приведенного выше признака Даламбера. Если существует предел Пример. Определить сходимость ряда
Вывод: ряд сходится. Пример. Определить сходимость ряда
Вывод: ряд сходится.
Признак Коши. (радикальный признак)
Если для ряда
то ряд
то ряд Следствие. Если существует предел
Пример. Определить сходимость ряда
Вывод: ряд сходится. Пример. Определить сходимость ряда
Т.е. признак Коши не дает ответа на вопрос о сходимости ряда. Проверим выполнение необходимых условий сходимости. Как было сказано выше, если ряд сходится, то общий член ряда стремится к нулю.
таким образом, необходимое условие сходимости не выполняется, значит, ряд расходится.
Интегральный признак Коши.
Если j(х) – непрерывная положительная функция, убывающая на промежутке [1;¥), то ряд j(1) + j(2) + …+ j(n) + … =
Пример. Ряд Следствие. Если f(x) и j(х) – непрерывные функции на интервале (a, b] и
Знакопеременные ряды. Знакочередующиеся ряды. Знакочередующийся ряд можно записать в виде:
Признак Лейбница. Если у знакочередующегося ряда Абсолютная и условная сходимость рядов.
Рассмотрим некоторый знакопеременный ряд (с членами произвольных знаков).
и ряд, составленный из абсолютных величин членов ряда (1):
Теорема. Из сходимости ряда (2) следует сходимость ряда (1). Определение. Ряд Очевидно, что для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают.
Определение. Ряд
Признаки Даламбера и Коши для знакопеременных рядов.
Пусть Признак Даламбера. Если существует предел Признак Коши. Если существует предел
Свойства абсолютно сходящихся рядов.
1) Теорема. Для абсолютной сходимости ряда Следствие. Условно сходящийся ряд является разностью двух расходящихся рядов с неотрицательными стремящимися к нулю членами. 2) В сходящемся ряде любая группировка членов ряда, не изменяющая их порядка, сохраняет сходимость и величину ряда. 3) Если ряд сходится абсолютно, то ряд, полученный из него любой перестановкой членов, также абсолютно сходится и имеет ту же сумму. Перестановкой членов условно сходящегося ряда можно получить условно сходящийся ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд. 4) Теорема. При любой группировке членов абсолютно сходящегося ряда (при этом число групп может быть как конечным, так и бесконечным и число членов в группе может быть как конечным, так и бесконечным) получается сходящийся ряд, сумма которого равна сумме исходного ряда. 5) Если ряды Если же производить перемножение условно сходящихся рядов, то в результате можно получить расходящийся ряд.
Функциональные последовательности.
Определение. Если членами ряда будут не числа, а функции от х, то ряд называется функциональным. Исследование на сходимость функциональных рядов сложнее исследования числовых рядов. Один и тот же функциональный ряд может при одних значениях переменной х сходиться, а при других – расходиться. Поэтому вопрос сходимости функциональных рядов сводится к определению тех значений переменной х, при которых ряд сходится. Совокупность таких значений называется областью сходимости. Так как пределом каждой функции, входящей в область сходимости ряда, является некоторое число, то пределом функциональной последовательности будет являться некоторая функция:
Определение. Последовательность { fn(x) } сходится к функции f(x) на отрезке [a,b], если для любого числа e>0 и любой точки х из рассматриваемого отрезка существует номер N = N(e, x), такой, что неравенство
выполняется при n>N. При выбранном значении e>0 каждой точке отрезка [a,b] соответствует свой номер и, следовательно, номеров, соответствующих всем точкам отрезка [a,b], будет бесчисленное множество. Если выбрать из всех этих номеров наибольший, то этот номер будет годиться для всех точек отрезка [a,b], т.е. будет общим для всех точек. Определение. Последовательность { fn(x) } равномерно сходится к функции f(x) на отрезке [a,b], если для любого числа e>0 существует номер N = N(e), такой, что неравенство
выполняется при n>N для всех точек отрезка [a,b].
Пример. Рассмотрим последовательность Данная последовательность сходится на всей числовой оси к функции f(x)=0, т.к.
При увеличении числа n график последовательности приближается к оси х.
Функциональные ряды.
Определение. Частными (частичными) суммами функционального ряда Определение. Функциональный ряд Определение. Совокупность всех значений х, для которых сходится ряд Определение. Ряд
Теорема. (Критерий Коши равномерной сходимости ряда) Для равномерной сходимости ряда
выполнялось бы для всех х на отрезке [a,b]. Пример. Исследовать на сходимость ряд Так как При этом известно, что общегармонический ряд Пример. Исследовать на сходимость ряд На отрезке [-1,1] выполняется неравенство
Степенные ряды.
Определение. Степенным рядом называется ряд вида
Для исследования на сходимость степенных рядов удобно использовать признак Даламбера. Пример. Исследовать на сходимость ряд Применяем признак Даламбера:
Получаем, что этот ряд сходится при Теперь определим сходимость в граничных точках 1 и –1. При х = -1: При х = 1: Теоремы Абеля. (Нильс Хенрик Абель (1802 – 1829) – норвежский математик) Теорема. Если степенной ряд Следствие. Если при х = х1 ряд расходится, то он расходится для всех Таким образом, для каждого степенного ряда существует такое положительное число R, что при всех х таких, что Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым. Радиус сходимости может быть найден по формуле:
Пример. Найти область сходимости ряда Находим радиус сходимости Следовательно, данный ряд сходится при любом значении х. Общий член этого ряда стремится к нулю.
Теорема. Если степенной ряд
Ряды Фурье. (Жан Батист Жозеф Фурье (1768 – 1830) – французский математик)
Тригонометрический ряд.
Определение. Тригонометрическим рядом называется ряд вида:
или, короче, Действительные числа ai, bi называются коэффициентами тригонометрического ряда. Если ряд представленного выше типа сходится, то его сумма представляет собой периодическую функцию с периодом 2p, т.к. функции sin nx и cos nx также периодические функции с периодом 2p. Пусть тригонометрический ряд равномерно сходится на отрезке [-p; p], а следовательно, и на любом отрезке в силу периодичности, и его сумма равна f(x). Определим коэффициенты этого ряда. Для решения этой задачи воспользуемся следующими равенствами:
Справедливость этих равенств вытекает из применения к подынтегральному выражению тригонометрических формул. Т.к. функция f(x) непрерывна на отрезке [-p; p], то существует интеграл
Такой результат получается в результате того, что
Далее умножаем выражение разложения функции в ряд на cos nx и интегрируем в пределах от -p до p.
Аналогично умножаем выражение разложения функции в ряд на sin nx и интегрируем в пределах от -p до p.
Выражение для коэффициента а0 является частным случаем для выражения коэффициентов an. Таким образом, если функция f(x) – любая периодическая функция периода 2p, непрерывная на отрезке [-p; p] или имеющая на этом отрезке конечное число точек разрыва первого рода, то коэффициенты
существуют и называются коэффициентами Фурье для функции f(x). Определение. Рядом Фурье для функции f(x) называется тригонометрический ряд, коэффициенты которого являются коэффициентами Фурье. Если ряд Фурье функции f(x) сходится к ней во всех ее точках непрерывности, то говорят, что функция f(x) разлагается в ряд Фурье. Разложение в ряд Фурье непериодической функции. Задача разложения непериодической функции в ряд Фурье в принципе не отличается от разложения в ряд Фурье периодической функции. Допустим, функция f(x) задана на отрезке [a, b] и является на этом отрезке кусочно – монотонной. Рассмотрим произвольную периодическую кусочно – монотонную функцию f1(x) c периодом 2Т ³ ïb-aï;, совпадающую с функцией f(x) на отрезке [a, b]. Таким образом, функция f(x) была дополнена. Теперь функция f1(x) разлагается в ряд Фурье. Сумма этого ряда во всех точках отрезка [a, b] совпадает с функцией f(x), т.е. можно считать, что функция f(x) разложена в ряд Фурье на отрезке [a, b]. Таким образом, если функция f(x) задана на отрезке, равном 2p ничем не отличается от разложения в ряд периодической функции. Если же отрезок, на котором задана функция, меньше, чем 2p, то функция продолжается на интервал (b, a + 2p) так, что условия разложимости в ряд Фурье сохранялись. Вообще говоря, в этом случае продолжение заданной функции на отрезок (интервал) длиной 2p может быть произведено бесконечным количеством способов, поэтому суммы получившихся рядов будут различны, но они будут совпадать с заданной функцией f(x) на отрезке [a,b].
Ряд Фурье для четных и нечетных функций.
Отметим следующие свойства четных и нечетных функций: 1) 2) Произведение двух четных и нечетных функций является четной функцией. 3) Произведение четной и нечетной функций – нечетная функция. Справедливость этих свойств может быть легко доказана исходя из определения четности и нечетности функций. Если f(x) – четная периодическая функция с периодом 2p, удовлетворяющая условиям разложимости в ряд Фурье, то можно записать:
Таким образом, для четной функции ряд Фурье записывается:
Аналогично получаем разложение в ряд Фурье для нечетной функции:
Пример. Разложить в ряд Фурье периодическую функцию Заданная функция является нечетной, следовательно, коэффициенты Фурье ищем в виде:
Получаем:
Построим графики заданной функции и ее разложения в ряд Фурье, ограничившись первыми четырьмя членами ряда.
Ряды Фурье для функций любого периода.
Ряд Фурье для функции f(x) периода Т = 2l, непрерывной или имеющей конечное число точек разрыва первого рода на отрезке [- l, l ] имеет вид:
Для четной функции произвольного периода разложение в ряд Фурье имеет вид:
Для нечетной функции:
|

 (2)
(2)



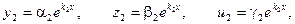
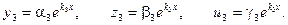


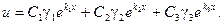





 (принимается любое значение), получаем:
(принимается любое значение), получаем: 

 Полагая
Полагая 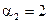 (принимается любое значение), получаем:
(принимается любое значение), получаем: 


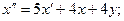






 Обозначив
Обозначив  , получаем решение системы:
, получаем решение системы:  называется числовым рядом.
называется числовым рядом. 
 будем называть членами ряда, а un – общим членом ряда.
будем называть членами ряда, а un – общим членом ряда. , n = 1, 2, … называются частными (частичными) суммами ряда.
, n = 1, 2, … называются частными (частичными) суммами ряда.
 и
и  , где С – постоянное число.
, где С – постоянное число. . Суммой или разностью этих рядов будет называться ряд
. Суммой или разностью этих рядов будет называться ряд  , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
, где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.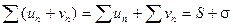
 была сходящейся, необходимо и достаточно, чтобы для любого
была сходящейся, необходимо и достаточно, чтобы для любого 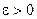 существовал такой номер N, что при n > N и любом p > 0, где р – целое число, выполнялось бы неравенство:
существовал такой номер N, что при n > N и любом p > 0, где р – целое число, выполнялось бы неравенство: .
. .
.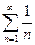 является расходящимся, хотя его общий член и стремится к нулю.
является расходящимся, хотя его общий член и стремится к нулю.
 - необходимый признак сходимости не выполняется, значит ряд расходится.
- необходимый признак сходимости не выполняется, значит ряд расходится.
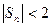 при любом n.
при любом n.
 , а гармонический ряд
, а гармонический ряд 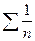 расходится, то расходится и ряд
расходится, то расходится и ряд  .
.
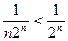 , а ряд
, а ряд  сходится (как убывающая геометрическая прогрессия), то ряд
сходится (как убывающая геометрическая прогрессия), то ряд  тоже сходится.
тоже сходится. и существует предел
и существует предел  , где h – число, отличное от нуля, то ряды
, где h – число, отличное от нуля, то ряды  то ряд
то ряд  то ряд
то ряд  , то при r < 1 ряд сходится, а при r > 1 – расходится. Если r = 1, то на вопрос о сходимости ответить нельзя.
, то при r < 1 ряд сходится, а при r > 1 – расходится. Если r = 1, то на вопрос о сходимости ответить нельзя. .
.
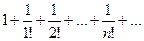

 ,
,
 , то при r<1 ряд сходится, а при r>1 ряд расходится.
, то при r<1 ряд сходится, а при r>1 ряд расходится. .
.
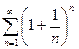 .
.
 ,
, и несобственный интеграл
и несобственный интеграл 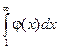 одинаковы в смысле сходимости.
одинаковы в смысле сходимости.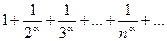 сходится при a>1 и расходится a£1 т.к. соответствующий несобственный интеграл
сходится при a>1 и расходится a£1 т.к. соответствующий несобственный интеграл  сходится при a>1 и расходится a£1. Ряд
сходится при a>1 и расходится a£1. Ряд  называется общегармоническим рядом.
называется общегармоническим рядом. то интегралы
то интегралы  и
и  ведут себя одинаково в смысле сходимости.
ведут себя одинаково в смысле сходимости. где
где 
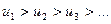 и общий член стремится к нулю
и общий член стремится к нулю  , то ряд сходится.
, то ряд сходится. (1)
(1)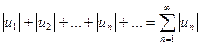 (2)
(2) .
. , то при r<1 ряд
, то при r<1 ряд 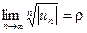 , то при r<1 ряд
, то при r<1 ряд  и
и  сходятся абсолютно и их суммы равны соответственно S и s, то ряд, составленный из всех произведений вида
сходятся абсолютно и их суммы равны соответственно S и s, то ряд, составленный из всех произведений вида  взятых в каком угодно порядке, также сходится абсолютно и его сумма равна S×s - произведению сумм перемножаемых рядов.
взятых в каком угодно порядке, также сходится абсолютно и его сумма равна S×s - произведению сумм перемножаемых рядов.



 называются функции
называются функции 
 называется суммой ряда
называется суммой ряда 
 .
. всегда, то очевидно, что
всегда, то очевидно, что  .
. .
. т.е. по признаку Вейерштрасса на этом отрезке исследуемый ряд сходится, а на интервалах (-µ, -1) È (1, µ) расходится.
т.е. по признаку Вейерштрасса на этом отрезке исследуемый ряд сходится, а на интервалах (-µ, -1) È (1, µ) расходится. .
.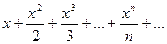
 .
. и расходится при
и расходится при  .
. ряд сходится по признаку Лейбница (см. Признак Лейбница.).
ряд сходится по признаку Лейбница (см. Признак Лейбница.). ряд расходится (гармонический ряд).
ряд расходится (гармонический ряд). .
. .
.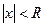 ряд абсолютно сходится, а при всех
ряд абсолютно сходится, а при всех  ряд расходится. При этом число R называется радиусом сходимости. Интервал (-R, R) называется интервалом сходимости.
ряд расходится. При этом число R называется радиусом сходимости. Интервал (-R, R) называется интервалом сходимости.

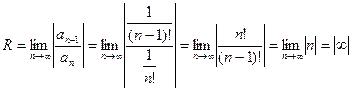

 сходится для положительного значения х=х1, то он сходится равномерно в любом промежутке внутри
сходится для положительного значения х=х1, то он сходится равномерно в любом промежутке внутри  .
.





 .
. Получаем:
Получаем: 
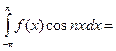

 Отсюда получаем:
Отсюда получаем: 
 Получаем:
Получаем: 


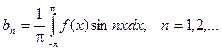








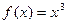 с периодом T = 2p на отрезке [-p;p].
с периодом T = 2p на отрезке [-p;p].



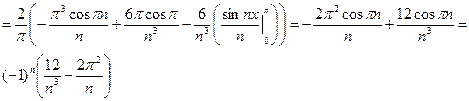

 .
.










