ББК 32.973 20 страница
Таблица 13
Однако двинемся дальше. В 1489 г. в учебнике арифметики Яна Видмана впервые в печатном издании появились символы + и –, введенные чуть раньше немецкими алгебраистами (коссистами). Франсуа Виет (1540—1603) придумал знаки для произвольных величин, называемых сегодня параметрами, и предложил правило: неизвестные обозначать гласными буквами, а параметры — согласными (табл. 14). Таблица 14
В табл. 14 planum и solidum — паразитные слова, которые можно безболезненно опустить[26]. Сделав это, получим
Последнее выражение можно легко понять с помощью переводной табл. 15. Нетрудно видеть, что запись уравнений у Виета неэргономична, громоздка и словообильна. Таблица 15
Тем не менее дело потихоньку двигалось вперед. Английский математик Р. Рекорд (1510—1558) придумал знак равенства =. Томас Гарриот (умер в 1621 г.) сделал следующий эргономический шаг, полностью исключив словесные описания. Уравнение aaa – 3. baa + 3. bba = 2. bbb Следующее эргономическое новшество принадлежит Рене Декарту. Он обозначил неизвестные величины буквами х, у, z, а известные — буквами a, b, c и ввел обозначения степеней: х 3, х 4, а 3, а 4. Правда, квадраты он иногда выражал с помощью символов xx, aa. Обозначение корня несколько отличается от современного: знак ОСОЗНАНИЕ ПОЛЕЗНОСТИ Подведем некоторые итоги. Эргономизация алгебры очень важна. Как отмечает голландский историк математики Дирк Стройк, “новые результаты часто становятся возможными лишь благодаря новому способу записи... Подходящее обозначение лучше отображает действительность, чем неудачное, оно оказывается как бы наделенным собственной жизненной силой, которая в свою очередь порождает новое. За усовершенствованием алгебраических обозначений Виета поколение спустя последовало применение алгебры к геометрии у Декарта” [6]. С ним согласен В. Катасонов: «Весь XVI век проходит под знаком настойчивых поисков удобной (читай — эргономичной!) алгебраической символики, которая позволила бы создать некое “исчисление” для решения задач... без излишней траты умственных сил, механически следуя простым правилам». Суть эргономизации алгебры не только и не столько в том, что она выработала очень компактные и достаточно удобные обозначения, но прежде всего в том, что эргономичные знаки и (что самое главное) их эргономичные комбинации образуют эргономичные зрительные сцены (диосцены), которые точно и строго отражая математическую реальность, вместе с тем гораздо лучше согласуются с нейробиологическими характеристиками человеческого глаза и мозга, что создает важные предпосылки для улучшения творческой продуктивности человеческого ума. Известно, что “прогресс науки... связан с созданием и совершенствованием символики. В свою очередь, сам этот прогресс зависит от того, насколько компактна и совершенна та знаковая система, которая отображает существенные свойства и черты реальности” [7]. Конечно, каждый отдельно взятый символ не может играть слишком большой роли. Но вся совокупность символов в целом, взаимоотношения между которыми складываются по вполне определенным правилам, — это уже целый язык, новая знаковая система. В таком едином ансамбле знакам присущи новые эргономические и иные свойства, которых не имеет каждый из них в отдельности. Эргономическая сущность замены словесных описаний на эффективные и компактные алгебраические формулы состоит в том, что происходит “удивительная рационализация визуального поля” [7]. В результате в оптическом поле одномоментного восприятия, визуального охвата оказывается значительно большая информация в удобной и доступной для восприятия форме. Это означает, что имеет место эффект симультанизации, который, как мы знаем, является одним из наиболее мощных рычагов, обеспечивающих ускорение работы мозга. Согласно взглядам Лазаря Карно, математические знаки “не являются только записью мысли, средством ее изображения и закрепления, — нет, они воздействуют на саму мысль, направляют ее и бывает достаточно переместить их на бумаге согласно известным, очень простым правилам, чтобы безошибочно достигнуть новых истин”. Логика знаковых преобразований наталкивает людей “на глубокие, не всегда привычные взаимосвязи явлений” [7]. Кроме того эргономизация алгебры включает в себя все ходы мысли, связанные с дроблением и вычленением новых понятий, доведением их до логического совершенства. Приведем пример. Алгебра Декарта неэргономична еще и потому, что он использовал неудачное определение понятия “коэффициент”, полагая, что все буквенные коэффициенты в алгебраических формулах положительны. Это ограничение имело вредные последствия. Например, если p > 0 и q > 0, уравнение в записи Декарта полностью отвечает современным требованиям и является вполне эргономичным (если забыть про неудачный знак равенства):
Если же знак коэффициента произволен, Декарт вводит странные многоточия [4]:
Эти никому не нужные многоточия, усложняющие символику, являются следствием неудачного определения понятия “буквенный коэффициент”. Чтобы устранить недостаток, надо улучшить определение, т. е. сделать его более эргономичным. Для этого будем считать, что буквы в уравнениях обозначают любое действительное число[27]. При таком определении нелепые многоточия становятся ненужными и исчезают, превращаясь (как и положено) в знаки + и –. Данный пример показывает, что эргономизация понятий в свою очередь может оказывать благотворное влияние на эргономичность обозначений. ЭРГОНОМИЧЕСКАЯ ПОБЕДА ЛЕЙБНИЦА Понятие эргономизации является универсальным: оно применимо не только к алгебре, но и ко многим другим вопросам. Чтобы убедиться в этом, рассмотрим еще один пример, связанный с эргономизацией исчисления бесконечно малых. Почти одновременное изобретение дифференциального и интегрального исчислений Лейбницем и Ньютоном явилось восхитительным достижением. Однако в противоположность удобным обозначениям Лейбница символика Ньютона оказалась громоздкой и эргономически неудачной. К чему это привело? Как пишет историк математики М. Кроу, “общее мнение британских математиков XIX в. состояло в том, что Ньютон был гением идеи, а Лейбниц — не только гением идеи, но и гением символики. Стремясь построить “всеобщую характеристику” (универсальный язык), он пришел ко многим новшествам в математических обозначениях. Лейбниц — один из самых плодовитых изобретателей математических символов. Немногие так хорошо понимали единство формы и содержания. Именно это внимание к знаку, к формальной стороне метода позволило Лейбницу сформулировать ряд важных положений математического анализа: это и знаменитая формула Лейбница для дифференцирования произведения, и многое другое. Только со времен Лейбница в математике стали широко использоваться знаки “·”, “:” для умножения и деления. Он же ввел в обиход символы log, ∫, d для логарифма, интеграла и дифференциала. Символы Лейбница настолько ясно выражали смысл и значение новых понятий, что легко привились и стали общепринятыми [6, 7]. Речь, разумеется, идет не только о выборе одиночных обозначений (буквенных или иных), но прежде всего о правилах построения суперзнаков. Мы используем термин “суперзнак” для обозначения правил комбинирования одиночных символов и правил их взаимного расположения в двумерном поле бумажной страницы, позволяющих получить полезный формальный или смысловой результат. Таким образом, суперзнак — это диосцена либо ее смысловой фрагмент. Примером суперзнака является выражение
а также любые формулы или цепочки формул, частью которых является указанное выражение[28]. Лейбниц хорошо понимал, что создание эффективных знаков и суперзнаков и пользование ими заключает в себе огромные возможности. Как бы предвосхищая будущие достижения когнитивной эргономики и семиотики, открывающие и облегчающие путь к мощным интеллектуальным прорывам, он пишет: “Общее искусство знаков, или искусство обозначения представляет собой чудесное пособие, так как оно разгружает воображение... Следует заботиться о том, чтобы обозначения были удобны для открытий. Это большей частью бывает, когда обозначения коротко выражают и как бы отображают интимнейшую суть вещей. Тогда поразительным образом сокращается работа мысли”. Поучителен известный спор Лейбница с Вагнером. Лейбниц. Удобная символика очень много значит для науки. Возражение Вагнера. Умный справится с любой задачей и без вспомогательных средств, а неумному не помогут никакие руководства. Ответ Лейбница. Я уверен, что плохая голова, упражняясь в использовании вспомогательных средств [знаков], может превзойти самую лучшую, подобно тому как ребенок может провести линию по линейке лучше, чем самый искусный мастер от руки. Гениальные же умы, снабженные такими преимуществами, пошли бы несравненно дальше. Школа Лейбница была “гораздо более блестящей, чем школа Ньютона” [6]. Что касается эргономически неудачной символики Ньютона, то она потерпела полный крах. Впрочем, поначалу деканы Кембриджа и Оксфорда рассматривали любую попытку своих студентов использовать обозначения Лейбница как нечестивый бунт против священной тени Ньютона. В итоге ньютонова школа в Англии и школа Лейбница на континенте настолько разошлись, что Леонард Эйлер в своем “Интегральном исчислении” (1768 г.) рассматривал объединение обоих способов записи, как бесполезное. Но эта преграда была сломлена в 1812 г. группой молодых кембриджских математиков, среди которых был и Чарльз Бэббедж, которого иногда называют отцом современной вычислительной техники. Они пытались, говоря словами Бэббеджа, проповедовать принципы чистого d -изма[29] в противоположность университетскому dotage (игра слов: dotage — старческое слабоумие; с другой стороны, МЕТОДОЛОГИЧЕСКАЯ ОШИБКА История математики показывает, что многие разделы этой науки стали успешно разрабатываться только после того, как были введены удобные (эргономичные) знаки, способствующие развитию соответствующих рассуждений и построений. Так, Джузеппе Пеано настаивал на важном значении символического обозначения во всяком математическом предложении, его полезности в трудных и тонких вопросах. Стефен Клини совершенно правильно отмечает: “Открытие простых символических обозначений, которые сами приводят к манипуляциям по формальным правилам, явилось одним из путей, на которых развивалась мощь современной математики”. Отсюда вытекает, что длительный исторический процесс изобретения, изменения, улучшения и реконструкции математической символики нельзя рассматривать как нечто второстепенное для математических исканий. Данный процесс (эргономический по своей природе) в немалой степени отражает волнующий путь зарождения и развития новых математических идей и понятий, он теснейшим образом связан с сокровенными тайнами математического творчества. Изучение названного эргономического процесса должно стать одним из важных направлений истории математики, если она хочет претендовать на статус научной дисциплины, удовлетворяющей современным междисциплинарным требованиям. К сожалению, в работах по истории науки в целом (и по истории математики в частности) эта сторона дела нередко выпадает из поля зрения ученых. Во многих публикациях господствует “модернизаторский” подход, когда старинные формулы и чертежи грубо искажаются в результате некритического перевода на современный язык. При этом эргономическая драма древних обозначений и понятий полностью ускользает от внимания исследователя. Например, в работе Б. Спасского даже чертеж Галилея, при помощи которого тот решал свою задачу, сильно изменен и упрощен и все изложение ведется на современном языке [9]. Отто Нейгебауэр довольно резко замечает: “Только в последнее время ученые, вслед за А. Ромом и А. Делаттом, начали публиковать тексты вместе с рисунками и обозначениями на них. Кроме этих недавних исключений, ни одному изданию верить нельзя, во всяком случае в отношении вида, буквенных обозначений и даже наличия рисунков” [10]. Пример сознательно модернизированного издания — Арифметика Диофанта. Например, символ Диофанта □ (неопределенный квадрат) переделан на понятный современному читателю лад х 2(переменная x Модернизированные издания древних математических рукописей позволяют быстро проследить ход решения задач и математических преобразований в современных обозначениях. Однако достигается это слишком дорогой ценой. Важнейшая задача историко-математического исследования — реконструкция математического мировоззрения древних авторов — остается невыполненной, так как отказ от старинных обозначений зачастую до неузнаваемости искажает старинную систему понятий. Другой недостаток состоит в том, что исследователь, упуская из виду междисциплинарный характер стоящей перед ним задачи, как бы “перепрыгивает” через ее самый трудный участок (который можно охарактеризовать как историко-эргономический анализ эволюции математических понятий и символики) и тем самым полностью лишает себя возможности выявить и тщательно исследовать эргономическую суть проблемы. В результате историко-математическое исследование не достигает цели и по крайней мере частично превращается в неумышленную фальшивку. АНАЛОГИЯ МЕЖДУ МАТЕМАТИЧЕСКОЙ Вспомним некоторые сведения из “классической” эргономики. Рассмотрим работу оператора, управляющего реакторным отделением атомной электростанции. Оператор трудится за пультом управления, на котором — наряду с другим оборудованием — размещается комплекс средств отображения информации, обеспечивающий выдачу оператору итоговой информации о работе реактора в виде, удобном для использования. Средства отображения информации представляют оператору возможность работать с информационной моделью объекта (реактора), которая должна быть адекватна реальной ситуации и соответствовать закономерностям и характеристикам человеческого восприятия, памяти, мышления. Модель должна быть наглядной, чтобы позволить человеку-оператору понять суть проблемной ситуации быстро, без трудоемкого анализа. При этом информация должна предъявляться человеку в “разжеванном виде” и не требовать от него дополнительного перекодирования в более понятную форму [11]. На основании теоретического анализа и обширного практического опыта специалисты по эргономике разработали многочисленные и весьма ценные правила, которым должна удовлетворять форма представления информации для человека-оператора [11, 12]. А теперь зададим вопрос: есть ли что-либо общее у двух, казалось бы, столь непохожих объектов, как панель отображения информации и страница математического текста? Оказывается, есть, причем можно указать четыре общих свойства. Во-первых, и панель индикации, и Исходя из сказанного, можно сделать четыре вывода. ! Система “математик — математический текст” в определенном отношении похожа на систему “оператор — средства отображения ! Математический текст и отображаемая на пульте информация являются аналогами, ибо представляют собой разные формы кодирования оптической информации, предназначенной для зрительного восприятия. ! Чтобы улучшить понимаемость математического текста, следует попытаться использовать разработанные в инженерной психологии эргономические правила, применяемые при проектировании средств отображения информации. ! В тех случаях, когда указанные правила “не работают”, следует доработать и улучшить когнитивно-эргономическую теорию, расширив ее возможности применительно к проектированию интересующих нас систем “человек—знание” (рис. 139). МАТЕМАТИЧЕСКАЯ И ЭРГОНОМИЧЕСКАЯ Вся математическая литература по определению представляет собой диоинформацию. Математические знания, которые мы получаем при помощи компьютерного экрана, принтера и плоттера, — это тоже диоинформация. Таким образом, в 99% случаев человек получает математические знания в форме диоинформации. Учитывая этот факт и опираясь на положения нового когнитивного подхода (см. гл. 5), можно предложить семь тезисов. Тезис 1. В подавляющем большинстве случаев математические идеи, теории и методы (за исключением тривиальных) становятся достоянием математического сообщества после представления их в письменном виде, предназначенном для визуального восприятия, т. е. после того, как математическая мысль приобрела форму диоинформации. Тезис 2. Математическая диоинформация — совокупность диосцен, каждую из которых можно рассматривать как суперзнак. Суперзнак — осмысленная двумерная комбинация знаков, целиком находящаяся в поле зрения. Тезис 3. Математическая диосцена обладает двумя фундаментальными свойствами. Во-первых, она несет определенное смысловое содержание и отображает математическую реальность. Во-вторых, это оптическая зрительная сцена, предназначенная для зрительного восприятия человеком. Тезис 4. Отсюда вытекает, что форма математической диосцены есть объект двойного назначения. Во-первых, отражая математическую реальность, она должна обеспечить выполнение формальных операций со знаками, преобразование знаков по определенным правилам, позволяющим получить полезный математический результат. Во-вторых, именно форма знаков и суперзнаков позволяет получить конечный результат зрительного восприятия, понимание человеком сущности математических идей и преобразований. Тезис 5. Разрушение или искажение формы приводит к двум “катастрофам”: 1) математическое содержание пропадает, превращаясь в ничто, в бессмыслицу; 2) осмысленное восприятие человеком математической диосцены рассыпается, понимание исчезает, а сама диосцена воспринимается как абсурдный набор бессодержательных пятен и линий.
Тезис 6. Следует различать два понятия: 1) математическая эффективность диосцены; 2) эргономическая эффективность диосцены. Первая имеет место, если диосцены и связанные с ними математические идеи и знаковые системы позволяют получить полезный математический результат, удовлетворяющий критерию математической строгости и другим разумным математическим критериям. Эргономическая эффективность имеет место, если удовлетворяется эргономический критерий Декарта, т. е. если человек может ценою минимальных интеллектуальных усилий либо воспринять и усвоить математическое содержание последовательности диосцен (если речь идет об изучении математического материала), либо с помощью указанных диосцен решить соответствующую математическую задачу (если речь идет не об изучении, а о решении новых задач). Тезис 7. Органический, принципиально неустранимый дефект понятия математической эффективности состоит в том, что оно почти полностью игнорирует проблему понимаемости математических текстов и связанный с нею критерий Декарта. Если на земном шаре отыщется пара суперматематиков, способных понять новую сложную математическую идею, этого вполне достаточно, чтобы дать ей путевку в жизнь. (При этом “мучения” всех остальных специалистов и студентов, связанные с трудностями понимания, категорически не принимаются в расчет.) Понятие эргономической эффективности математики вводится для того, чтобы облегчить и упростить процесс понимания сложных математических проблем, создать научную основу для введения понятия “производительность математического труда” и на этой основе обеспечить реальное повышение продуктивности работы ума математиков, а также миллионов людей, изучающих эту сложную науку. Утрируя, можно предложить вымышленный диалог. — Почему математика такая трудная? — Потому что до сих пор никто не пытался создать научно-обоснованный метод, позволяющий сделать ее более легкой. КАК ПОВЫСИТЬ ПРОИЗВОДИТЕЛЬНОСТЬ МАТЕМАТИЧЕСКОГО ТРУДА? Развитие математики и логики увенчалось созданием богатого набора формальных правил, использование которых позволяет решать обширный класс математических и логических задач. При разработке этих правил математики преследовали две цели. Первая цель была основной и явно выраженной: обогатить математическое знание. Вторая цель состояла в том, чтобы сделать знаковые системы и математические преобразования по возможности удобными и обозримыми. Эта вторая (эргономическая) цель была скорее интуитивной, чем осознанной и научно обоснованной. В настоящее время, когда сложность математических знаний превысила “критический порог”, настало время коренным образом изменить подход к проблеме. В математике следует выделить два набора правил: ! традиционную математическую и логико-математическую формализацию, обеспечивающую достижение математической эффективности; ! набор эргономических формальных правил, цель которых — добиться эргономической эффективности математических методов. Необходимо “уравнять в правах” и объединить оба набора. В итоге получим единый набор формальных правил, для обозначения которых выше предложен термин “когнитивная формализация знаний”. Совместное применение правил позволит получить удвоенный выигрыш. Суть вопроса в том, что повышение производительности математического труда, понимаемое как повышение продуктивности человеческого мозга (мозга математиков), — не столько математическая, сколько эргономическая проблема. Человеческий ум и методы улучшения его работы — предмет изучения не математики, а когнитивной эргономики. Эту мысль следует подчеркнуть особо: эргономический выигрыш в математике есть не что иное как повышение производительности математического труда. Когнитивная формализация как научная идея, направленная на улучшение работы человеческого ума, — это новорожденный младенец, делающий самые первые шаги, но которому, по нашему мнению, суждено большое будущее. ДВА МЕТОДА ВИЗУАЛИЗАЦИИ Математический текст в общем случае строится из трех “строительных блоков”:
История математики показывает, что по мере развития математических знаний часть словесного текста постепенно заменяется формулами и изображениями. Указанная замена представляет собой один из важных аспектов эргономизации математики, так как при этом сукцессивное (медленное) восприятие текста заменяется симультанным (быстрым) восприятием формул и изображений. Важным, хотя и не единственным методом математической эргономизации следует признать визуализацию (замену текста изображением), которая, как отмечает С. Клименко, призвана “делать видимым невидимое”. Повышение интереса к визуализации породило в США инициативу VISC (Visualization in Scientific Computing), что означает “визуализация в научных вычислениях” [12]. Визуализация математики — это обширная область исследований, охватывающая большое число разнообразных способов и приемов. Среди них выделим два, которые назовем формальным и неформальным методами. Примером формального метода визуализации является визуальный синтаксис языка ДРАКОН. В самом деле, сравнивая левую и правую части на рис. 90, 91, легко убедиться, что текстовые и визуальные формулы, во-первых, являются строго формальными, во-вторых, эквивалентны друг другу. Другим примером формального подхода служит развитие визуального программирования в CASE -технологиях и компьютерных методологиях, а также когнитивной компьютерной графики. В последнем случае используются так называемые “когнитивные изображения”, позволяющие показать “внутреннее содержание, идею, суть изображаемого оригинала, которым может быть любое абстрактное научное понятие, гипотеза или теория” [13]. По мнению А. Зенкина, использовавшего идеи когнитивной графики для формального и весьма плодотворного исследования хорошо известной в математике классической проблемы Варинга и ряда других вопросов, этот метод дает возможность “прямого воздействия на сам процесс интуитивного образного мышления исследователя”, в связи с чем “эффективность человеческого мышления, прежде всего в процессе научного познания, способна возрасти уже на многие порядки” [13]. Формальные методы визуализации математики обладают чрезвычайно большим творческим потенциалом. Вместе с тем они имеют очевидный недостаток: каждый такой метод является “штучным произведением искусства”, он появляется на свет в результате индивидуального творческого акта и — в общем случае — не дает никаких прямых указаний, никакой явной подсказки, позволяющей поставить дело на поток и “штамповать” подобные изобретения в массовом порядке на воображаемом “математическом конвейере”. От этого недостатка свободен неформальный метод математической визуализации, о котором пойдет речь ниже. ПРОЕКТ “КОГНИТИВНЫЙ СТИЛЬ” Было бы крайне желательно предложить простой и универсальный визуально-эргономический метод, позволяющий сделать более понятной и наглядной любую или почти любую сложную абстрактную математическую идею или задачу. Одним из возможных подходов к проблеме является метод CogniStyle. Согласно предварительному, пока еще не завершенному проекту он представляет собой универсальный метод визуализации научной и учебной литературы, который, в частности, можно применить для визуализации произвольных математических текстов. Все без исключения рисунки в этой книге спроектированы методом CogniStyle. Для примера перечислим несколько наиболее простых эргономических приемов из набора CogniStyle.
|


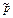

 A cubus + B in A 7 aequatur C
A cubus + B in A 7 aequatur C в записи Гарриота имело “почти современный” вид
в записи Гарриота имело “почти современный” вид означает у Декарта кубический корень. Есть и другие недостатки: Декарт “испортил” знак равенства, изображая его как µ [4].
означает у Декарта кубический корень. Есть и другие недостатки: Декарт “испортил” знак равенства, изображая его как µ [4].
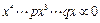
 ,
, ) [6]. Справедливости ради добавим, что символика Ньютона полностью не исчезла: с позором изгнанная из математического анализа, она тем не менее иногда применяется в теоретической механике.
) [6]. Справедливости ради добавим, что символика Ньютона полностью не исчезла: с позором изгнанная из математического анализа, она тем не менее иногда применяется в теоретической механике.



