Действия над комплексными числами
Пусть заданы числа:
1. Сложение:
2. Вычитание:
3. Умножение:
4. Деление:
Замечание: умножение и деление производят не по конечным формулам, а реализуют процесс.
5. Равенство:
Натуральная и целая степени комплексного числа определяются также, как и для действительных чисел.
Модуль и аргумент комплексного числа. Тригонометрическая форма записи комплексного числа
Каждому комплексному числу на комплексной плоскости соответствует точка
Модулем комплексного числа Модуль числа Аргументом комплексного числа Все аргументы числа Главным значением аргумента называется значение аргумента, удовлетворяющее условию Для комплексного числа
Но при этом необходимо учитывать расположение числа Частные случаи:
Тригонометрическая форма записи комплексного числа:
где
|

 ,
, .
. ;
; ;
;
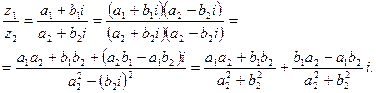
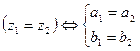 .
. .
.
 называется величина
называется величина  и обозначается
и обозначается  .
. равен расстоянию от начала координат до точки
равен расстоянию от начала координат до точки  , изображающей это число.
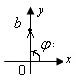
, изображающей это число. между положительным направлением оси
между положительным направлением оси  и вектором, соответствующим данному числу. Причем величина угла берется со знаком «+», если отсчет ведется против часовой стрелки, и со знаком «-» – если по часовой.
и вектором, соответствующим данному числу. Причем величина угла берется со знаком «+», если отсчет ведется против часовой стрелки, и со знаком «-» – если по часовой. и обозначаются
и обозначаются  .
. или
или  и обозначается
и обозначается  .
. величина
величина  может быть найдена из соотношения
может быть найдена из соотношения .
. .
.





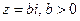



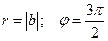 или
или 

 модуль комплексного числа;
модуль комплексного числа;  аргумент комплексного числа.
аргумент комплексного числа.


