Вычисление объемов тел вращения.
Пусть требуется вычислить объем тела вращения вокруг оси OX. Тогда Аналогично, объем тела вращения вокруг оси OY, если функция задана в виде Если функция задана в виде
Переходя к дифференциалу и пренебрегая квадратичными членами, имеем ВОПРОС Вычисление длины дуги Длина ломаной линии, которая соответствует дуге, может быть найдена как Тогда длина дуги равна Из геометрических соображений: Если дуга задана в полярной системе координат, то
Площадь поверхности тела вращения. Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.
Разобьем дугу АВ на n частей точками M0, M1, M2, …, Mn. Координаты вершин полученной ломаной имеют координаты xi и yi. При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна DPi. Эта площадь может быть найдена по формуле:
Здесь DSi – длина каждой хорды.
Применяем теорему Лагранжа (см. Теорема Лагранжа.) к отношению Получаем: Тогда
Площадь поверхности, описанной ломаной равна:
Эта сумма не является интегральной, но можно показать, что
Тогда 28 вопрос
Пусть функция f(x) определена и непрерывна на интервале [a, ¥). Тогда она непрерывна на любом отрезке [a, b]. Определение: Если существует конечный предел Обозначение:
Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится. Если предел не существует или бесконечен, то несобственный интеграл расходится.
Аналогичные рассуждения можно привести для несобственных интегралов вида:
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.
|

 .
. , можно вычислить по формуле
, можно вычислить по формуле  .
. и требуется определить объем тела вращения вокруг оси OY, то формулу для вычисления объема можно получить следующим образом.
и требуется определить объем тела вращения вокруг оси OY, то формулу для вычисления объема можно получить следующим образом.
 . Интегрируя и применяя формулу Ньютона – Лейбница, имеем
. Интегрируя и применяя формулу Ньютона – Лейбница, имеем  .
. .
. .
.
 . Поэтому
. Поэтому  .
.

 .
.




 - формула вычисления площади поверхности тела вращения.
- формула вычисления площади поверхности тела вращения.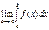 , то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).
, то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).





