В декартовой системе координат.
Мы пришли к понятию определенного интеграла от задачи о площади криволинейной трапеции (фактически, используя метод интегральных сумм). Если функция Но функция может на некотором отрезке принимать и отрицательные значения, тогда интеграл по этому отрезку будет давать отрицательную площадь, что противоречит определению площади. Можно вычислять площадь по формуле S= 2. Фигура ограничена графиком функции, заданной в полярной системе координат.
Пусть график функции задан в полярной системе координат и мы хотим вычислить площадь криволинейного сектора, ограниченного двумя лучами Здесь можно использовать метод интегральных сумм, вычисляя площадь криволинейного сектора как предел суммы площадей элементарных секторов, в которых график функции заменен дугой окружности Можно использовать и метод дифференциалов: Заменяя элементарный криволинейный сектор, соответствующий центральному углу
26 Вычисление объемов Пусть имеется тело объема V. Площадь любого поперечного сечения тела Q, известна как непрерывная функция Q = Q(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки хi разбиения отрезка [a, b]. Т.к. на каком- либо промежуточном отрезке разбиения [xi-1, xi] функция Q(x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно Mi и mi. Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны MiDxi и miDxi здесь Dxi = xi - xi-1. Произведя такие построения для всех отрезков разбиения, получим цилиндры, объемы которых равны соответственно При стремлении к нулю шага разбиения l, эти суммы имеют общий предел:
Таким образом, объем тела может быть найден по формуле:
Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию Q(x), что весьма проблематично для сложных тел.
|

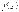 принимает только неотрицательные значения, то площадь
принимает только неотрицательные значения, то площадь  под графиком функции на отрезке [a, b] может быть вычислена с помощью определенного интеграла
под графиком функции на отрезке [a, b] может быть вычислена с помощью определенного интеграла  . Заметим, что
. Заметим, что  поэтому здесь можно увидеть и метод дифференциалов.
поэтому здесь можно увидеть и метод дифференциалов.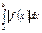 . Это равносильно изменению знака функции в тех областях, в которых она принимает отрицательные значения.Если надо вычислить площадь фигуры, ограниченной сверху графиком функции
. Это равносильно изменению знака функции в тех областях, в которых она принимает отрицательные значения.Если надо вычислить площадь фигуры, ограниченной сверху графиком функции  , а снизу графиком функции
, а снизу графиком функции  , то можно пользоваться формулой S=
, то можно пользоваться формулой S=  , так как
, так как  .
. и графиком функции
и графиком функции  в полярной системе координат.
в полярной системе координат. .
. .
. круговым сектором, имеем пропорцию
круговым сектором, имеем пропорцию  . Отсюда
. Отсюда  . Интегрируя и используя формулу Ньютона – Лейбница, получаем
. Интегрируя и используя формулу Ньютона – Лейбница, получаем 
 .
.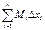 и
и 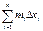 .
.




