Цилиндрическая система координат.
Связь координат произвольной точки Р пространства в цилиндрической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:
Для представления тройного интеграла в цилиндрических координатах вычисляем Якобиан:
Итого:
Сферическая система координат.
Связь координат произвольной точки Р пространства в сферической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:
Для представления тройного интеграла в сферических координатах вычисляем Якобиан:
Окончательно получаем:
38 вопрос
Корни многочлена Как мы видели выше, методом выделения полного квадрата можно найти корни квадратного трехчлена. В случае многочленов высших степеней найти корни становится гораздо труднее, а иногда и просто невозможно. Попробуем это сделать там, где это достаточно просто. Рассмотрим многочлен Доказательство Действительно, если число
39 вопрос свойства: 1) Криволинейный интеграл при перемене направления кривой меняет знак. 2) 3) 4) 5) Криволинейный интеграл по замкнутой кривой L не зависит от выбора начальной точки, а зависит только от направления обхода кривой.
|






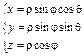



 где a 1, a 2,..., a n − целые числа, a n ≠ 0. Теорема о рациональных корнях многочлена Если многочлен
где a 1, a 2,..., a n − целые числа, a n ≠ 0. Теорема о рациональных корнях многочлена Если многочлен  с целыми коэффициентами имеет рациональный корень
с целыми коэффициентами имеет рациональный корень  то число p является делителем числа
то число p является делителем числа  (свободного члена), а число q является делителем числа
(свободного члена), а число q является делителем числа  (старшего коэффициента).
(старшего коэффициента). является корнем многочлена
является корнем многочлена  то
то  а именно:
а именно:  Умножим обе части этого уравнения на
Умножим обе части этого уравнения на 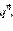 получим:
получим:  Так как
Так как  − целые числа, то в скобке стоит целое число. Значит, вся правая часть этого равенства делится на q, так как q входит в неё в качестве сомножителя. А значит и левая часть тождества делится на q, так как она равна правой. Число p не делится на q, так как иначе дробь
− целые числа, то в скобке стоит целое число. Значит, вся правая часть этого равенства делится на q, так как q входит в неё в качестве сомножителя. А значит и левая часть тождества делится на q, так как она равна правой. Число p не делится на q, так как иначе дробь  была бы сократимой, значит и
была бы сократимой, значит и  не делится на q. Следовательно, на q делится единственный из оставшихся сомножителей левой части, а именно
не делится на q. Следовательно, на q делится единственный из оставшихся сомножителей левой части, а именно  Аналогично доказывается, что
Аналогично доказывается, что 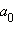 делится на p. Теорема доказана.
делится на p. Теорема доказана.







