Среднего профессионального образования
Дизайн-студия «Сплайн»
Ярославль, Клубная, 48
www.sd-spline.ru
Государственное образовательное учреждение
Медицинский колледж №2 Рабочая тетрадь Лекции №4
по теме: «Основные понятия дискретной математики. Закон больших чисел. Теория вероятностей» предмет: «Математика» специальность: «Лечебное дело» - 060101-52 Составитель: Короткова Е.В.
Москва 2009 г. Тема: Основные понятия дискретной математики. Элементы теории вероятностей. Общая цель: изучить основные понятия дискретной математики и теории вероятностей и применять их при решении задач. Конкретные цели. Студент должен знать: · элементы математической логики; · определение факториала; · основные понятия комбинаторики: перестановки, размещения, сочетания; · понятие случайного события, частоты события, вероятности события; · основные теоремы и формулы теории вероятности; · определение математического ожидания и дисперсии случайной величины; · закон больших чисел. Студент должен уметь: · производить операции дизъюнкции, конъюнкции, отрицания; · находить число размещений, перестановок, сочетаний; · находить сумму (объединение), произведение (пересечение) событий, вероятность событий; · применять основные теоремы и формулы при нахождении вероятности события, математического ожидания и дисперсии случайной величины. План. 1. Понятие множества. Способы задания множеств. 2. Операции над множествами. 3. Элементы математической логики. 4. Основные понятия комбинаторики. 5. Определение вероятности события. 6. Основные теоремы и формулы теории вероятностей. 7. Случайные величины. Математическое ожидание. Дисперсия. Закон больших чисел. Литература: 1. С.Г. Григорьев. Математика. Гл.5. п.5.1.1, 5.1.2, 5.1.3. Стр.213-216. И.Д.Пехлецкий. Математика. Гл.1. п.1.1.Стр.11-14. 2. С.Г. Григорьев. Математика. Гл.5. п.5.1.1, 5.1.2, 5.1.3. Стр.213-216. И.Д.Пехлецкий. Математика. Гл.1. п.1.1.Стр.11-14. 3. С.Г. Григорьев. Математика. Гл.5. п.5.2. Стр.222-226. 4. С.Г. Григорьев. Математика. Гл.7. п.7.2. Стр.2264-266. И.Д.Пехлецкий. Математика. Гл.10. п.10.2.Стр.208-210. 5. С.Г. Григорьев. Математика. Гл.7. п.7.1. Стр.259-262. И.Д.Пехлецкий. Математика. Гл.10..Стр.200-204. 6. С.Г. Григорьев. Математика. Гл.7. п.7.3. Стр.267-272, п.7.4.Стр.274- 278, п.7.5.Стр.282,283.
1. Синонимы: ________________ _________________________ _________________________ _________________________
Примеры множеств: ______________
Множество может содержать конечное или бесконечное число объектов произвольной природы.
Объекты – это ____________________ _________________________________
________________________________ ________________________________ Х = Y
____________________________
________________________________ ________________________________ ________________________________ ________________________________
Множество называется упорядоченным, __________________________________
__________________________________
Существует три способа задания множеств.
1). ____________________________________________________________________ Пример: _______________________________________________________________ 2). ____________________________________________________________________ Пример: _______________________________________________________________ 3). ____________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ _______________________________________________________________________ Пример: _______________________________________________________________ _______________________________________________________________________
множеств А и В называется _____________ ______________________________________ ______________________________________
ОПРЕДЕЛЕНИЕ. Пересечением двух множеств А и В называется _____________ ______________________________________ ______________________________________
ОПРЕДЕЛЕНИЕ. Декартовым произведением множеств А и В называется _______________________________________________________________________ _______________________________________________________________________ Пример: _______________________________________________________________ _______________________________________________________________________
ОПРЕДЕЛЕНИЕ. Высказыванием называется _______________________________________ ________________________________________
_______________________________ _______________________________
Обозначение: __________________________ 2+2=10
предложения, предложения которые служат
|









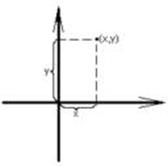
 Y ________________________________
Y ________________________________


 __________________________________
__________________________________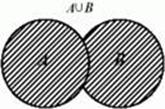 2. ОПРЕДЕЛЕНИЕ. Объединением двух
2. ОПРЕДЕЛЕНИЕ. Объединением двух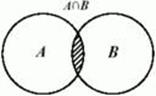
 3.
3. Примеры: ______________________________
Примеры: ______________________________
 Вопросительные, восклицательные
Вопросительные, восклицательные


