Мода – чаще всего встречающаяся значение признака. В дискретном ряду определяется по наибольшей частоте. В интервальном по формуле:
 - начальное знач. интервала, содержащего моду;
 - величина модального интервала;  - частота модального интервала;   - частота интервала, предшествующего (следующег) модальному;
| Медиана – значение признака, приходящегося на середину ранжированной совокупности.
 
 — начальное значение интервала, содержащего медиану;
 — величина медианного интервала;  — сумма частот ряда;
 — сумма накопленных частот, предшествующих медианному интервалу;  — частота медианного интервала.
|
Характер распределения признака в совокупности:
Мо=Ме=  - симметричное; Мо<Ме< правосторонняя ассиметрия; Мо>Ме> - левосторонняя ассиметрия
|
Квартили значение признака, делящие ранжированную совокупность на четыре части.
Квинтили - на пять равных частей, Децили - на 10, Перцентили на 100.
Показатели вариации (для оценки типичности средней и характера распределения)
| Абсолютные
| Что показывает
|
1. Размах вариации 
| границы вариации
|
| 2. Среднее линейное отклонение
|
| 
| величина отклонения признака от средней Абстрогированность от знака
|
| 3. Дисперсия среднее квадратическое отклонение.-средний квадрат отклонений признака от средней
|
|  ; 
| мерило средней, чем меньше, тем лучше средняя отражает совокупность. Не имеет единиц измерения.
|
| 4. Среднее квадратическое отклонение
|
|
| 
| Характеристика колеблемости признака
|
| Относительные
|
1. Коэффициент осцилляции 
| Колеблемость крайних значений признака вокруг средней
|
2. Относительное линейное отклонение 
| Доля усредненного значения абсолютных отклонений от средней
|
3. Коэффициент вариации 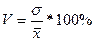 , характеризует однородность,> 35% совокупность не однородна
|
Коэффициент ассиметрии Пирсона  ; Показатель эксцесса  >0,островершинен, <0,низковершинен
>0,островершинен, <0низковершинен
|
