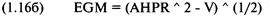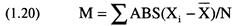Как разброс результатов затрагивает геометрический рост

После того как мы признали тот факт, что, хотим мы того или нет, сознательно или нет, количество для торговли определяется по уровню баланса на счете, можно рассматривать HPR, а не денежные суммы. Таким образом, мы прида­дим управлению деньгами определенность и точность. Мы сможем проверить наши стратегии управления деньгами, составить правила и сделать определен­ные выводы. Посмотрим, как связан геометрический рост и разброс результа­тов (HPR).

В этой дискуссии мы для простоты будем использовать пример азартной игры. Рассмотрим две системы: систему А, которая выигрывает 10% времени и имеет отношение выигрыш/проигрыш 28 к 1, и систему В, которая выигрывает 70% времени и имеет отношение выигрыш/проигрыш 1,9 к 1. Наше математическое ожидание на единицу ставки для А равно 1,9, а для В равно 0,4. Поэтому мы мо­жем сказать, что для каждой единицы ставки система А выиграет, в среднем, в 4,75 раз больше, чем система В. Но давайте рассмотрим торговлю фиксирован­ной долей. Мы можем найти оптимальные f, разделив математическое ожидание на отношение выигрыш/проигрыш. Это даст нам оптимальное f = 0,0678 для А и 0,4 для В. Средние геометрические для каждой системы при соответствующих значениях оптимальных f составят:

 

А= 1,044176755

В= 1,0857629

Как видите, система В, несмотря на то что ее математическое ожидание пример­но в четыре раза меньше, чем системы А, приносит почти в два раза больше за ставку (доходность 8,57629% за ставку, когда вы реинвестируете с оптимальным f), чем система А (которая приносит 4,4176755% за ставку, когда вы реинвести­руете с оптимальным f).

 

Система	% Выигрышей	Выигрыш: Проигрыш	МО	f	Среднее геометрическое
А		28: 1	1,9	0,0678	1,0441768
В		1,9:1	0,4	0,4	1,0857629

 

Проигрыш 50% по балансу потребует 100% прибыли для возмещения; 1,044177 в степени Х будет равно 2,0, когда Х приблизительно равно 16,5, то есть для возме­щения 50% проигрыша для системы А потребуется более 16 сделок. Сравним с сис­темой В, где 1,0857629 в степени Х будет равно 2,0, когда Х приблизительно равно 9, то есть для системы В потребуется 9 сделок для возмещения 50% проигрыша.

В чем здесь дело? Не потому ли все это происходит, что система В имеет про­цент выигрышных сделок выше? Истинная причина, по которой В функциони­рует лучше А, кроется в разбросе результатов и его влиянии на функцию роста. Большинство трейдеров ошибочно считают, что функция роста TWR задается следующим образом:

где R = процентная ставка за период (например, 7% = 0,07);

N = количество периодов.

Так как 1 + R то же, что и HPR, большинство ошибочно полагает, что функция роста1 TWR равна:

(1.18) TWR = HPR ^N

 

Эта функция верна только тогда, когда прибыль (то есть HPR) постоянна, чего в торговле не бывает. Реальная функция роста в торговле (или любой другой среде, где HPR не явля­ется постоянной) — это произведение всех HPR. Допустим, мы торгуем кофе, наше оптимальное f составляет 1 контракт на каждую 21 000 долларов на балансе счета и прошло 2 сделки, одна из которых принесла убыток 210 долларов, а другая выигрыш 210 долларов. В этом примере HPR равны 0,99 и 1,01 соответственно. Таким образом, TWR равно:

TWR = 1,01 * 0,99 = 0,9999

Дополнительную информацию можно получить, используя оценочное среднее геометрическое (EGM):

или

Теперь возведем уравнение (1.16а) или (1.166) в степень N, чтобы рассчитать TWR Оно будет близко к «мультипликативной» функции роста, действительному TWR

или

где N = количество периодов;

АНPR = среднее арифметическое HPR;

SD = стандартное отклонение значений HPR;

V = дисперсия значений HPR.

Оба уравнения (1.19) эквивалентны.

Полученная информация говорит, что найден компромисс между увели­чением средней арифметической торговли (HPR) и дисперсией HPR, и ста­новится ясна причина, по которой система (1,9:1; 70%) работает лучше, чем система (28:1; 10%)!

Нашей целью является максимизация коэффициента этой функции, т.е. мак­симизация следующей величины:

Показатель оценочного TWR, т.е. N, сам о себе позаботится. Увеличение N не яв­ляется проблемой, так как мы можем расширить количество рынков или торго­вать в более краткосрочных типах систем.

Расчет дисперсии и стандартного отклонения (V и SD соответственно) может оказаться трудным для большинства людей, не знакомых со статистикой. Вместо этих величин многие используют среднее абсолютное отклонение, которое мы на­зовем М. Чтобы найти М, надо просто взять среднее абсолютное значение разно­сти самой величины и ее среднего значения.

При колоколообразном распределении (как почти всегда бывает с распределени­ем прибылей и убытков торговой системы) среднее абсолютное отклонение при­мерно равно 0,8 стандартного отклонения (в нормальном распределении оно со­ставляет 0,7979). Поэтому мы можем сказать:

и

Обозначим среднее арифметическое HPR переменной А, а среднее геометричес­кое HPR переменной G. Используя уравнение (1.166), мы можем выразить оце­ночное среднее геометрическое следующим образом:

Из этого уравнения получим:

Теперь вместо дисперсии подставим стандартное отклонение [как в (1.16а)]:

Из этого уравнения мы можем выделить каждую переменную, а также выде­лить ноль, чтобы получить фундаментальные соотношения между средним арифметическим, средним геометрическим и разбросом, выраженным здесь как SD ^{^} 2:

В этих уравнениях значение SD^2 можно записать как V или как (1,25 * М) ^2. Это подводит нас к той точке, когда мы можем описать существующие взаимо­связи. Отметьте, что последнее из уравнений — это теорема Пифагора: сумма квад­ратов катетов равна квадрату гипотенузы! Но здесь гипотенуза это А, а мы хотим максимизировать одну из ее сторон, G. При увеличении G любое повышение D («катет» дисперсии, равный SD или V^(1/2), или 1,25 * М) приведет к увеличению А. Когда D равно нулю, тогда А равно G, этим самым соответствуя ложно толкуе­мой функции роста TWR = (1 + R)^ N. Действительно, когда D равно нулю, тогда А равно G в соответствии с уравнением (1.26).

Мы можем сказать, что повышение А^ 2 оказывает на G то же воздей­ствие, что и аналогичное понижение величины (1,25 * М) ^ 2.

Чтобы понять это, рассмотрим изменение А от 1,1 до 1,2:

А	SD	М	G	А^2	SD ^ 2 = (1, 25 * М)^ 2
1,1	0,1	0,08	1,095445	1,21	0,01
1,2	0,4899	0,39192	1,095445	1.44	0.24
					0,23 =	0,23

 

Когда A=l,l,ToSD=0,l. Когда А = 1,2, то, чтобы получить эквивалентное G, SD должно быть равно 0,4899, согласно уравнению (1.27). Так как М = = 0,8 * SD,ToM=0,3919. Если мы возведем в квадрат значения А и SD и рассчитаем раз­ность, то получим 0,23 в соответствии с уравнением (1.29). Рассмотрим следующую таблицу:

А		SD	М	G	А^2	SD ^ 2 = (1,25 * М) ^ 2
1,1		0,25	0,2	1,071214	1, 21		0,0625
1,2		0,5408	0,4327	1,071214	1, 44		0.2925
					0, 23	=	0,23

 

Отметьте, что в предыдущем примере, где мы начали с меньших значений разбро­са (SD или М), требовалось их большее повышение, чтобы достичь того же G. Таким образом, можно утверждать, что чем сильнее вы уменьшаете дисперсию, тем легче дается больший выигрыш. Это экспоненциальная функция, причем в пределе, при ну­левой дисперсии, G равно А. Трейдер, который торгует на фиксированной долевой ос­нове, должен максимизировать G, но не обязательно А. При максимизации G надо понимать, что стандартное отклонение SD затрагивает G в той же степени, что и А в соответствии с теоремой Пифагора! Таким образом, когда трейдер уменьшает стан­дартное отклонение (SD) своих сделок, это эквивалентно повышению арифметичес­кого среднего HPR (т.е. А), и наоборот!