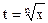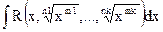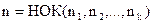Правило 1. Для вычисления интегралов вида
 ,
, 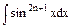
(n –целое положительное число) удобно ввести вспомогательную функцию sin x в первом случае и cos x – во втором.
Пример 1. 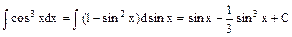
Пример 2. 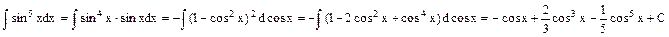
Для четных степеней sin x или cos x правило 1 не ведет к цели (см. правило 2).
Правило 2. Для вычисления интегралов вида: 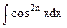 ,
, 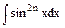
удобно пользоваться формулами: 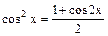 и
и 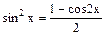
и вводить вспомогательную функцию cos2x.
Правило 3. Для вычисления интегралов вида 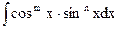 , где, по крайней мере, одно из чисел m, n – нечетное, удобно ввести вспомогательную функцию sin x (если m нечетно) или cos x (если n нечетно) и поступать так же, как в примерах 1, 2.
, где, по крайней мере, одно из чисел m, n – нечетное, удобно ввести вспомогательную функцию sin x (если m нечетно) или cos x (если n нечетно) и поступать так же, как в примерах 1, 2.
Правило 4.
Если m и n четные, то интегралы вида 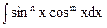 , (где m и n – натуральные числа) находятся с помощью тригонометрических формул:
, (где m и n – натуральные числа) находятся с помощью тригонометрических формул:
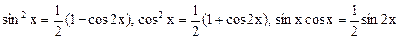
Правило 5.
Интегралы вида  , где
, где 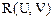 - рациональная функция двух аргументов U и V, сводится к интегралу от рациональной функции аргумента t подстановкой
- рациональная функция двух аргументов U и V, сводится к интегралу от рациональной функции аргумента t подстановкой 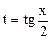 .
.
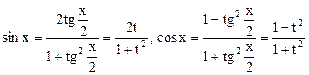
Из подстановки 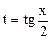 , следует что
, следует что 
Пример 6.
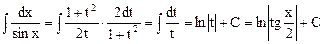
Интегрирование иррациональных выражений.
| №
| Тип интеграла
| Способ интегрирования
|
|
| 
| 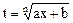
|
|
| 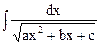
| Дополнение квадратного трехчлена до полного квадрата
|
|
| 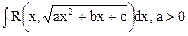
| Подстановка Эйлера: 
|
|
| 
| Подстановка Эйлера:
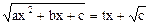
|
|
| 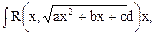 , , 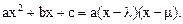
| Подстановка Эйлера: 
|
|
| 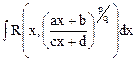
| Подстановка: 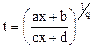
|
|
| 
| Подстановка: 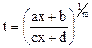 , , 
|
|
| 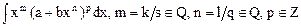
| Подстановка Чебышева:
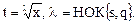
|
|
| 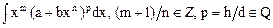
| Подстановка Чебышева:
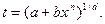
|
|
| 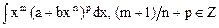
| Подстановка Чебышева:
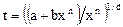
|
|
| 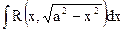
| 
|
|
| 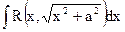
| 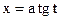
|
|
| 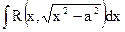
| 
|
|
| 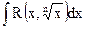 (частный случай интеграла (6)) (частный случай интеграла (6))
| 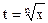
|
|
| 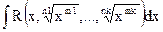
| 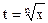 , где , где 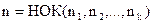
|

 ,
, 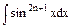
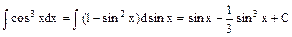
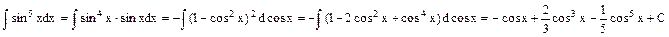
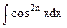 ,
, 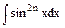
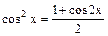 и
и 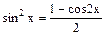
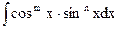 , где, по крайней мере, одно из чисел m, n – нечетное, удобно ввести вспомогательную функцию sin x (если m нечетно) или cos x (если n нечетно) и поступать так же, как в примерах 1, 2.
, где, по крайней мере, одно из чисел m, n – нечетное, удобно ввести вспомогательную функцию sin x (если m нечетно) или cos x (если n нечетно) и поступать так же, как в примерах 1, 2.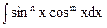 , (где m и n – натуральные числа) находятся с помощью тригонометрических формул:
, (где m и n – натуральные числа) находятся с помощью тригонометрических формул: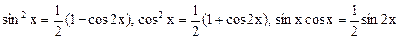
 , где
, где 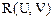 - рациональная функция двух аргументов U и V, сводится к интегралу от рациональной функции аргумента t подстановкой
- рациональная функция двух аргументов U и V, сводится к интегралу от рациональной функции аргумента t подстановкой 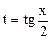 .
.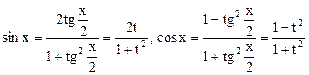

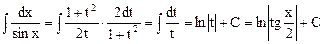

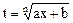
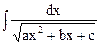
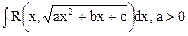


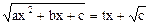
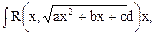 ,
, 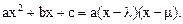

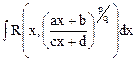
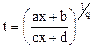

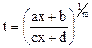 ,
, 
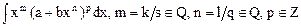
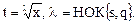
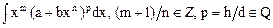
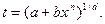
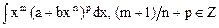
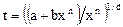
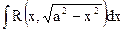

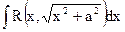
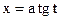
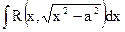

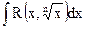 (частный случай интеграла (6))
(частный случай интеграла (6))