Методы интегрирования
(с лампами накаливания) TD 314 S WH MYYT
Применяется для освещения общественных и жилых помещений.
Светильники уличного освещения незаменимы в интерьере любого загородного дома: они помогут подсветить необходимые места Вашего участка, акцентировать некоторые его детали. Кроме того, с ними будет намного легче гулять в вечернее время на свежем воздухе. Также Вы можете украсить и осветить Ваши беседку, веранду или террасу с помощью встраиваемых светильников уличного освещения. Уличное освещение загородного дома, которое при правильности его планировки, установке и эксплуатации способна выгодно подчеркнуть, индивидуальность, органичность и красоту вашего дома.
Методы интегрирования
Интегрирование по частям – это интегрирование по формуле
Этот метод позволяет вычислять интегралы следующих видов (P(x) –многочлен): A. B. Пример 1. Вычислить интеграл Решение. Полагая U = 3x + 1, dV = e2xdx, находим dU = 3dx, V= 1/2e2x. Поэтому
Пример 2. Вычислить интеграл
Метод разложения заключается в том, что применение свойств 3 и 4 неопределенного интеграла позволяет свести исходный интеграл к табличным формулам. Пример 1. Возможности применения табличных формул связаны со свойством инвариантности интеграла (под знаком интеграла вместо х может стоять любая функция U(x)), то есть, если Пример 2. Метод замены переменной (метод подстановки). Замена переменной состоит в том, что вместо переменной x в подынтегральное выражение f(x)dx вводится функция причем в случае удачной замены последний интеграл проще исходного. Пример 1. Вычислить интеграл Решение. Введем новую переменную, положив t = 4x – 3, Сделаем обратную замену: Проверка: Непосредственное интегрирование. В простых случаях введение нового переменного можно выполнять в уме, применяя следующие преобразования дифференциала dx:
и обозначая мысленно выражение в скобках через U (применение свойства инвариантности интеграла). Пример 2.
|









 :
: 

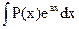 ,
,  ,
,  - берём P(x)=U
- берём P(x)=U ,
,  ,
,  - берём P(x)dx = dV.
- берём P(x)dx = dV. .
. .
.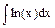 . Решение. Полагая U = ln(x), dV = dx, находим dU =
. Решение. Полагая U = ln(x), dV = dx, находим dU =  , V= x. Поэтому
, V= x. Поэтому 
 .
. , то
, то  .
. , так как
, так как  .
. . В результате получим
. В результате получим 
 . Внесем эти выражения под интеграл. Получим
. Внесем эти выражения под интеграл. Получим  .
. .
. .
. ;
; 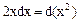 ;
;  ;
; 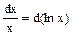 и т. п.,
и т. п.,



