Теоретическое введение. Инженерная экология – система научно обоснованных инженерно-технических мероприятий, призванная разрабатывать инженерные методы исследования экосистемы
Инженерная экология – система научно обоснованных инженерно-технических мероприятий, призванная разрабатывать инженерные методы исследования экосистемы «человек – окружающая среда», инженерно-технические методы и средства защиты человека и окружающей его среды от особо опасных, опасных и вредных антропогенных факторов. В качестве экологической системы «человек – производственный объект – окружающая среда» может рассматриваться любое промышленное предприятие, включающее в себя материальные, энергетические и людские ресурсы, занятые в производственном процессе. Такие системы характеризуются тем, что в зависимости от условий внешней среды могут принимать несколько состояний при одних и тех же начальных условиях. Поэтому для исследования таких систем должен быть применен системный подход. Проблема экологической безопасности в рамках производственного предприятия должна анализироваться в широком аспекте как комплексная задача обеспечения внутрипроизводственной безопасности и безвредности, а также защиты окружающей среды. Решение проблемы экологической безопасности производственных предприятий требует привлечения системы знаний, объединяющей на основе общей методологии, достижения в области безопасности труда, охраны окружающей среды и промышленной безопасности.
Лабораторная работа Соотношение неопределенностей для фотонов
Цель работы: экспериментальная проверка выполнения соотношения неопределенностей для фотонов. Приборы и принадлежности: источники излучения (лазеры ЛГН-113 и ZY 852), щель с микрометрической регулировкой ширины, оптическая скамья, экран, линейка рулетка.
Теоретическое введение Принцип неопределенностей, сформулированный на основе корпускулярно-волнового дуализма, является одним из фундаментальных принципов современной физики. Для квантовых частиц его можно сформулировать следующим образом. Неопределенность координатной составляющей частицы
где В данной работе соотношение неопределенности (1) проверяется экспериментально для фотонов. Как проявление принципа неопределенности в оптике можно трактовать явление дифракции. Действительно, состояние движения фотона вдоль оси Поскольку неопределенность проекции импульса
Учтем, что модуль импульса фотона излучения с длиной волны
Тогда величину неопределенности импульса (2) можно записать
Так как при дифракции основная доля излучения будет сосредоточена в максимуме нулевого порядка, то есть в диапазоне угловых расстояний от (
Из этого неравенства следует, что угловая расходимость светового пучка после дифракции на щели шириной Dх может быть оценена на основе равенства
Этот результат полностью соответствует результату классической теории дифракции, в которой расходимость излучения определяется на основе формулы
В формуле (5) угол
Сравнив формулы (5) и (6), получим выражение
которое для удобства анализа представим в виде
Таким образом, для проверки выполнения соотношения неопределенностей необходимо измерить ширину щели, принимаемую за неопределенность координаты фотона
|

 и неопределенность проекции импульса на то же направление
и неопределенность проекции импульса на то же направление  удовлетворяют соотношению
удовлетворяют соотношению , (1)
, (1) – постоянная Планка.
– постоянная Планка.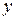 в области
в области  (рисунок 1) ничем не ограничено в пространстве. В этой области координат импульс фотона
(рисунок 1) ничем не ограничено в пространстве. В этой области координат импульс фотона  характеризуется вполне конкретными значениями координатных составляющих
характеризуется вполне конкретными значениями координатных составляющих  . В точке
. В точке  , в которой расположена входная щель, состояние движения фотона характеризуется пространственным ограничением по координате
, в которой расположена входная щель, состояние движения фотона характеризуется пространственным ограничением по координате  . Неопределенность координаты фотона
. Неопределенность координаты фотона  в окрестности значения
в окрестности значения 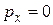 . Следовательно, в области пространства
. Следовательно, в области пространства  будут присутствовать фотоны, которые движутся не только в направлении оси
будут присутствовать фотоны, которые движутся не только в направлении оси  . (2)
. (2) определяется
определяется . (3)
. (3) . (4)
. (4) ) до
) до  (рисунок 1), то неопределенность выделенной проекции импульса можно принять равной
(рисунок 1), то неопределенность выделенной проекции импульса можно принять равной  . При этом произведение неопределенностей координаты и импульса будет удовлетворять соотношению
. При этом произведение неопределенностей координаты и импульса будет удовлетворять соотношению , или
, или 
 . (5)
. (5)


 (см. рисунок 1). Ввиду малости угла
(см. рисунок 1). Ввиду малости угла  . (6)
. (6) ,
, . (7)
. (7) .
.


