ОЦЕНКА ЗАГРЯЗНЕНИЯ ВОЗДУХА РАБОЧЕЙ ЗОНЫ
Эксплуатация БТТ фиксируется документально и систематически. Техническая документация на образцы вооружения и техники включает: ¾ формуляр машины; ¾ паспорт двигателя; ¾ комплектовочная ведомость; ¾ инструкция (памятка) по эксплуатации машины; ¾ паспорта на составляющие устройства (радиостанция, пулеметы, ПРХР и т.д.); ¾ инструкции (памятки) по эксплуатации составляющих устройств (радиостанции, ПРХР и т.д.). Технические службы и их задачи по организации эксплуатации БТВТ, автомобильной техники и военно-технического имущества в частях и подразделениях. В полку имеет три технические службы: ¾ бронетанковая служба (БТС); ¾ автомобильная служба (АС); ¾ служба ракетно-артиллерийского вооружения (СРАВ). Основными задачами технических служб полка являются: ¾ истребование недостающего ВВТ; ¾ обучение специалистов ремонтно-восстановительных органов; ¾ организация эксплуатации ВВТ; ¾ обеспечение военно-техническим имуществом подразделений полка. Порядок эксплуатации и установленные годовые нормы расхода моторесурсов бронетанкового вооружения на мирное время. Бронетанковое вооружение и техника должны использовать только по назначению. Порядок эксплуатации БТВТ определяется руководящими документами. КОЛИЧЕСТВО МАШИН ПО ГРУППАМ ЭКСПЛУАТАЦИИ И ГОДОВЫЕ НОРМЫ РАСХОДА МОТОРЕСУРСОВ
Гарантийные наработки и межремонтные ресурсы бронетанкового вооружения. Единицы учёта ресурса и наработки.
Ресурс машины измеряется в километрах пробега. Ресурс определяет пробег машины до:
¾ среднего ремонта; ¾ капитального ремонта.
Наработка машины измеряется в километрах (гарантийная, наработка до ТО№1 или ТО№2). Наработка составляющих устройств может измеряться в других единицах, например, двигателя – в моточасах, пулеметов – в выстрелах, радиостанции – в часах.
Использование бронетанкового вооружения в боевых условиях.
Бронетанковое вооружение в боевых условиях используется на основании Наставления по обеспечению боевых действий Сухопутных войск. Наработка машин определяется решения командира на бой (или сложившейся обстановкой).
ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ
- напоминаю тему и цели занятия; - определяю как достигнуты цели; - объявляю оценки; - произвожу разбор занятия; - объявляю тему следующего занятия; - отвечаю на вопросы обучаемых. Методическую разработку составил Старший преподаватель НИУ ВШЭ п/п–к Ю. ЧУМАЧЕНКО Модуль №2. Векторная алгебра Вариант 1
1. Векторы 1) 2. На плоскости даны точки А(-2,3); В(3,3); С(2,-2). В начале координат приложены силы 3. Разложить геометрически и аналитически вектор 4. Под действием силы 5. Даны векторы 1) ( 6. Даны векторы 1) ( 7. Найти площадь треугольника с вершинами A(4,2,-1); B(3,0,4); C(0,0,4). 8. Найти площадь параллелограмма, построенного на векторах 9. Даны три силы, приложенные к точке A(2,1,2) 10. Установить, компланарны ли векторы 11. Даны координаты вершин пирамиды A угол между ребрами A площадь грани A проекцию вектора объем пирамиды.
Вариант 2
1. Векторы 1) 2. На плоскости даны точки А(-1,5); В(3,5); С(4,-1). В начале координат приложены силы 3. Разложить геометрически и аналитически вектор 4. Под действием силы 5. Даны векторы 1) ( 6. Даны векторы 1) ( 7. Найти площадь треугольника с вершинами A(1,1,2); B(2,3,-1); C(2,-2,4). 8. Найти площадь параллелограмма, построенного на векторах
9. Сила 10. Установить, компланарны ли векторы 11. Даны координаты вершин пирамиды A A угол между ребрами A площадь грани A проекцию вектора объем пирамиды.
Вариант 3
1. Векторы 1) 2. На плоскости даны точки А(5,3); В(-2,4); С(3,-2). В начале координат приложены силы 3. Разложить геометрически и аналитически вектор 4. Под действием силы 5. Даны векторы 1) ( 6. Даны векторы Найти: 1) ( 7. Найти площадь треугольника с вершинами A(2,3,1); B(4,1,-2); C(6,3,7). 8. Найти площадь параллелограмма, построенного на векторах
9. Сила 10. Установить, компланарны ли векторы 11. Даны координаты вершин пирамиды A угол между ребрами A площадь грани A проекцию вектора объем пирамиды.
Вариант 4
1. Векторы 1) 2. На плоскости даны точки А(5,-2); В(2,4); С(-2,3). В начале координат приложены силы 3. Разложить геометрически и аналитически вектор 4. Под действием силы 5. Даны векторы 1) ( 6. Даны векторы Найти: 1) ( 7. Найти площадь треугольника с вершинами A(1, 3, 2); B(3, 2, 7); C(-2, 1, 2). 8. Найти площадь параллелограмма, построенного на векторах
9. Сила 10. Установить, компланарны ли векторы 11. Даны координаты вершин пирамиды A угол между ребрами A площадь грани A проекцию вектора объем пирамиды.
Вариант 5
1. Векторы 1) 2. На плоскости даны точки А(-2,5); В(3,5); С(5,-2). В начале координат приложены силы 3. Разложить геометрически и аналитически вектор 4. Под действием силы 5. Даны векторы 1) ( 6. Даны векторы 1) ( 7. Найти площадь треугольника с вершинами A(4,5,-2); B(-1,3,0); C(6,1,5). 8. Найти площадь параллелограмма, построенного на векторах
9. Сила 10. Установить, компланарны ли векторы
11. Даны координаты вершин пирамиды A угол между ребрами A площадь грани A проекцию вектора объем пирамиды.
Вариант 6
1. Векторы 2. На плоскости даны точки А(5,-3); В(-1,2); С(3,1). В начале координат приложены силы 3. Разложить геометрически и аналитически вектор 4. Под действием силы 5. Даны векторы 1) ( 6. Даны векторы 1) ( 7. Найти площадь треугольника с вершинами A(-3, -2, 0); B(3, -3, 1); C(5, 0, 2). 8. Найти площадь параллелограмма, построенного на векторах
9. Сила 10. Доказать, что четыре данные точки A(-3,-2,0); B(5,0,2); C(3,-3,1); D(-1,1,1) лежат в одной плоскости. 11. Даны координаты вершин пирамиды A угол между ребрами A площадь грани A проекцию вектора объем пирамиды.
Вариант 7
1. Векторы 1) 2. На плоскости даны точки А(-4, 2); В(2, 3); С(0, 5). В начале координат приложены силы 3. Разложить геометрически и аналитически вектор 4. Под действием силы 5. Даны векторы 1) ( 6. Даны векторы 1) ( 7. Найти площадь треугольника с вершинами A(3,3,-2); B(0,-3,4); C(0,-3,0). 8. Найти площадь параллелограмма, построенного на векторах
9. Сила 10. Установить, компланарны ли векторы 11. Даны координаты вершин пирамиды A угол между ребрами A площадь грани A
|

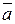 и
и  даны геометрически. Построить каждый из следующих векторов:
даны геометрически. Построить каждый из следующих векторов: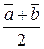 ; 2)
; 2)  ; 3)
; 3) 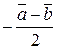 ; 4)
; 4) 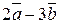 ;
;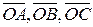 . Построить равнодействующую
. Построить равнодействующую  . Выразить силы
. Выразить силы  через единичные векторы
через единичные векторы  и
и  координатных осей. Найти величину равнодействующей
координатных осей. Найти величину равнодействующей 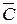 по векторам
по векторам  .
. ={2,-3,-1} материальная точка переместилась из точки A(2,-2,1) в точку B(7,-3,1). Вычислить работу силы
={2,-3,-1} материальная точка переместилась из точки A(2,-2,1) в точку B(7,-3,1). Вычислить работу силы 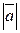 ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 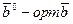 .
. где
где 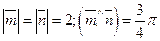 . Найти:
. Найти: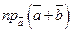 ;
;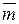 -3
-3  ;
;  =
=  ;
; 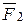 =
= 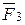 =-2
=-2 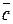 =
=  A
A 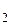 A
A 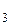 A
A  : A
: A  на
на 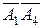
 ; 4)
; 4)  ;
; . Найти:
. Найти: ; 4)
; 4)  ;
;
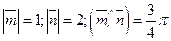 . Найти:
. Найти: ;
; +
+  ;
; 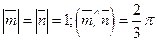 . Найти:
. Найти:


