Б1.В.ОД.10 Организация деятельности коммерческого банка
2. Теорема Коши. Пусть функции Доказательство:
Рассмотрим функцию F(x) непрерывна на [ a; b ] и дифференцируема в (a; b).
F(x) удовлетворяет условию теоремы Ролля, значит существует c Î (a; b) такая, что
3. Теорема Лагранжа (о конечных приращениях).
Доказательство: В теореме Коши выберем
На отрезке [ a; b ] всегда существует точка, касательная в которой параллельна секущей. Пример: доказать Выберем
СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ ЛАГРАНЖА: 1) Если Доказательство: Выберем произвольно x 1 < x 2:
Ввиду произвольности выбора x 1 и x 2 f(x) = const. 2) Если Доказательство:
Пример: доказать
4. Правило Лопиталя. Предел отношения двух бесконечно малых равен пределу отношений их производных, если последний существует.
Доказательство: Известно, что f(a) = 0, g(a) = 0, f(x) и g(x) дифференцируемы в окрестности точки a,
перейдем к пределу x ® a:
ЗАМЕЧАНИЯ: 1) Правило выполняется при x ®¥. 2) Правило выполняется, если f(x) ®0, g(x) ®0, при x ® a. 3) Правило выполняется, если f(x) ®¥, g(x) ®¥, при x ® a.
Пример: 1) 2) 3) 4) 5)
Б1.В.ОД.10 Организация деятельности коммерческого банка
Направление подготовки
|
и 
непрерывны на отрезке [ a; b ] и дифференцируемы в интервале (a; b) и 
для всех x Î (a; b), тогда 
хотя бы для одной c Î (a; b).
(по условию),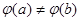 
, иначе 
удовлетворяет условию теоремы Ролля и существует c такая, что 
, что противоречит условию.
и докажем, что эта функция удовлетворяет условию теоремы Ролля.
.
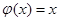, тогда теорема Коши будет иметь такой вид 
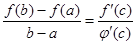, но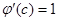 
, получим 
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ТЕОРЕМЫ ЛАГРАНЖА.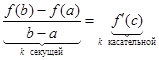
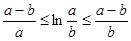, если 
.
и применим к ней теорему Лагранжа на отрезке [ a; b ], получим:
для любого x Î[ a; b ], то 
.
, то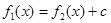 
.
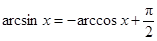, что требовалось доказать.
.
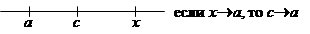
. Доказательство закончено.
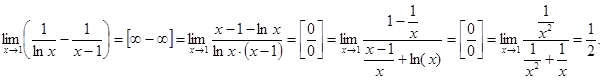
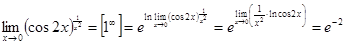, так как
